Expected Utility Forecasting for Science Funding
The typical science grantmaker seeks to maximize their (positive) impact with a limited amount of money. The decision-making process for how to allocate that funding requires them to consider the different dimensions of risk and uncertainty involved in science proposals, as described in foundational work by economists Chiara Franzoni and Paula Stephan. The Von Neumann-Morgenstern utility theorem implies that there exists for the grantmaker — or the peer reviewer(s) assessing proposals on their behalf — a utility function whose expected value they will seek to maximize.
Common frameworks for evaluating proposals leave this utility function implicit, often evaluating aspects of risk, uncertainty, and potential value independently and qualitatively. Empirical work has suggested that such an approach may lead to biases, resulting in funding decisions that deviate from grantmakers’ ultimate goals. An expected utility approach to reviewing science proposals aims to make that implicit decision-making process explicit, and thus reduce biases, by asking reviewers to directly predict the probability and value of different potential outcomes occurring. Implementing this approach through forecasting brings the added benefits of providing (1) a resolution and scoring process that could help incentivize reviewers to make better, more accurate predictions over time and (2) empirical estimates of reviewers’ accuracy and tendency to over or underestimate the value and probability of success of proposals.
At the Federation of American Scientists, we are currently piloting this approach on a series of proposals in the life sciences that we have collected for Focused Research Organizations (FROs), a new type of non-profit research organization designed to tackle challenges that neither academia or industry is incentivized to work on. The pilot study was developed in collaboration with Metaculus, a forecasting platform and aggregator, and is hosted on their website. In this paper, we provide the detailed methodology for the approach that we have developed, which builds upon Franzoni and Stephan’s work, so that interested grantmakers may adapt it for their own purposes. The motivation for developing this approach and how we believe it may help address biases against risk in traditional peer review processes is discussed in our article “Risk and Reward in Peer Review”.
Defining Outcomes
To illustrate how an expected utility forecasting approach could be applied to scientific proposal evaluation, let us first imagine a research project consisting of multiple possible outcomes or milestones. In the most straightforward case, the outcomes that could arise are mutually exclusive (i.e., only a single one will be observed). Indexing each outcome with the letter 𝑖, we can define the expected value of each as the product of its value (or utility; 𝓊𝑖) and the probability of it occurring, 𝑃(𝑚𝑖). Because the outcomes in this example are mutually exclusive, the total expected utility (TEU) of the proposed project is the sum of the expected value of each outcome1:
𝑇𝐸𝑈 = 𝛴𝑖𝓊𝑖𝑃(𝑚𝑖).
However, in most cases, it is easier and more accurate to define the range of outcomes of a research project as a set of primary and secondary outcomes or research milestones that are not mutually exclusive, and can instead occur in various combinations.
For instance, science proposals usually highlight the primary outcome(s) that they aim to achieve, but may also involve important secondary outcome(s) that can be achieved in addition to or instead of the primary goals. Secondary outcomes can be a research method, tool, or dataset produced for the purpose of achieving the primary outcome; a discovery made in the process of pursuing the primary outcome; or an outcome that researchers pivot to pursuing as they obtain new information from the research process. As such, primary and secondary outcomes are not necessarily mutually exclusive. In the simplest scenario with just two outcomes (either two primary or one primary and one secondary), the total expected utility becomes
𝑇𝐸𝑈 = 𝓊1𝑃(𝑚1⋂ not 𝑚2) + 𝓊2𝑃(𝑚2⋂ not 𝑚1) + (𝓊1 + 𝓊2)𝑃(𝑚1⋂𝑚2),
𝑇𝐸𝑈 = 𝓊1𝑃(𝑚1) – (𝑚1⋂ 𝑚2)) + 𝓊2𝑃(𝑚2) – 𝑃(𝑚1⋂ 𝑚2)) + (𝓊1 + 𝓊2)𝑃(𝑚1⋂𝑚2)
𝑇𝐸𝑈 = 𝓊1𝑃(𝑚1) + 𝓊2𝑃(𝑚2) – (𝓊1 + 𝓊2)𝑃(𝑚1⋂𝑚2).
As the number of outcomes increases, the number of joint probability terms increases as well. Assuming the outcomes are independent though, they can be reduced to the product of the probabilities of individual outcomes. For example,
𝑃(𝑚1⋂𝑚2) = 𝑃(𝑚1) * 𝑃(𝑚2)
On the other hand, milestones are typically designed to build upon one another, such that achieving later milestones necessitates the achievement of prior milestones. In these cases, the value of later milestones typically includes the value of prior milestones: for example, the value of demonstrating a complete pilot of a technology is inclusive of the value of demonstrating individual components of that technology. The total expected utility can thus be defined as the sum of the product of the marginal utility of each additional milestone and its probability of success:
𝑇𝐸𝑈 = 𝛴𝑖(𝓊𝑖 + 𝓊𝑖-1)𝑃(𝑚𝑖),
where 𝓊0 = 0.
Depending on the science proposal, either of these approaches — or a combination — may make the most sense for determining the set of outcomes to evaluate.
In our FRO Forecasting pilot, we worked with proposal authors to define two outcomes for each of their proposals. Depending on what made the most sense for each proposal, the two outcomes reflected either relatively independent primary and secondary goals, or sequential milestone outcomes that directly built upon one another (though for simplicity, we called all of the outcomes milestones).
Defining Probability of Success
Once the set of potential outcomes have been defined, the next step is to determine the probability of success between 0% and 100% for each outcome if the proposal is funded. A prediction of 50% would indicate the highest level of uncertainty about the outcome, whereas the closer the predicted probability of success is to 0% or 100%, the more certainty there is that the outcome will be one over the other.
Furthermore, Franzoni and Stephan decompose probability of success into two components: the probability that the outcome can actually occur in nature or reality and the probability that the proposed methodology will succeed in obtaining the outcome (conditional on it being possible in nature). The total probability is then the product of these two components:
𝑃(𝑚𝑖) = 𝑃nature(𝑚𝑖) * 𝑃proposal(𝑚𝑖)
Depending on the nature of the proposal (e.g., more technology-driven, or more theoretical/discovery driven), each component may be more or less relevant. For example, our forecasting pilot includes a proposal to perform knockout validation of renewable antibodies for 10,000 to 15,000 human proteins; for this project, 𝑃nature(𝑚𝑖) approaches 1 and 𝑃proposal(𝑚𝑖) drives the overall probability of success.
Defining Utility
Similarly, the value of an outcome can be separated into its impact on the scientific field and its impact on society at large. Scientific impact aims to capture the extent to which a project advances the frontiers of knowledge, enables new discoveries or innovations, or enhances scientific capabilities or methods. Social impact aims to capture the extent to which a project contributes to solving important societal problems, improving well-being, or advancing social goals.
In both of these cases, determining the value of an outcome entails some subjective preferences, so there is no “correct” choice, at least mathematically speaking. However, proxy metrics may be helpful in considering impact. Though each is imperfect, one could consider citations of papers, patents on tools or methods, or users of method, tools, and datasets as proxies of scientific impact. For social impact, some proxy metrics that one might consider are the value of lives saved, the cost of illness prevented, the number of job-years of employment generated, economic output in terms of GDP, or the social return on investment.
The approach outlined by Franzoni and Stephan asks reviewers to assess scientific and social impact on a linear scale (0-100), after which the values can be averaged to determine the overall impact of an outcome. However, we believe that an exponential scale better captures the tendency in science for a small number of research projects to have an outsized impact and provides more room at the top end of the scale for reviewers to increase the rating of the proposals that they believe will have an exceptional impact.
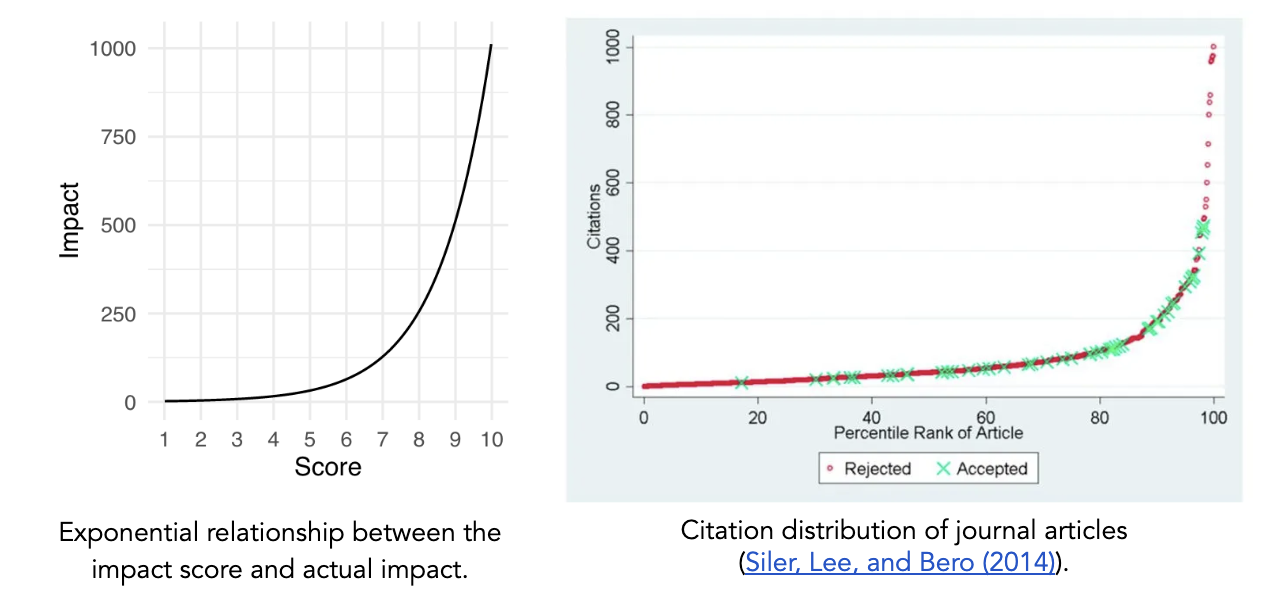
As such, for our FRO Forecasting pilot, we chose to use a framework in which a simple 1–10 score corresponds to real-world impact via a base 2 exponential scale. In this case, the overall impact score of an outcome can be calculated according to
𝓊𝑖 = log[2science impact of 𝑖 + 2social impact of 𝑖] – 1.
For an exponential scale with a different base, one would substitute that base for two in the above equation. Depending on each funder’s specific understanding of impact and the type(s) of proposals they are evaluating, different relationships between scores and utility could be more appropriate.
In order to capture reviewers’ assessment of uncertainty in their evaluations, we asked them to provide median, 25th, and 75th percentile predictions for impact instead of a single prediction. High uncertainty would be indicated by a narrow confidence interval, while low uncertainty would be indicated by a wide confidence interval.
Determining the “But For” Effect of Funding
The above approach aims to identify the highest impact proposals. However, a grantmaker may not want to simply fund the highest impact proposals; rather, they may be most interested in understanding where their funding would make the highest impact — i.e., their “but for” effect. In this case, the grantmaker would want to fund proposals with the maximum difference between the total expected utility of the research proposal if they chose to funded it versus if they chose not to:
“But For” Impact = 𝑇𝐸𝑈(funding) – 𝑇𝐸𝑈(no funding).
For TEU(funding), the probability of the outcome occurring with this specific grantmaker’s funding using the proposed approach would still be defined as above
𝑃(𝑚𝑖 | funding) = 𝑃nature(𝑚𝑖) * 𝑃proposal(𝑚𝑖),
but for 𝑇𝐸𝑈(no funding), reviewers would need to consider the likelihood of the outcome being achieved through other means. This could involve the outcome being realized by other sources of funding, other researchers, other approaches, etc. Here, the probability of success without this specific grantmaker’s funding could be described as
𝑃(𝑚𝑖 | no funding) = 𝑃nature(𝑚𝑖) * 𝑃other mechanism(𝑚𝑖).
In our FRO Forecasting pilot, we assumed that 𝑃other mechanism(𝑚𝑖) ≈ 0. The theory of change for FROs is that there exists a set of research problems at the boundary of scientific research and engineering that are not adequately supported by traditional research and development models and are unlikely to be pursued by academia or industry. Thus, in these cases it is plausible to assume that,
𝑃(𝑚𝑖 | no funding) ≈ 0
𝑇𝐸𝑈(no funding) ≈ 0
“But For” Impact ≈ 𝑇𝐸𝑈(funding).
This assumption, while not generalizable to all contexts, can help reduce the number of questions that reviewers have to consider — a dynamic which we explore further in the next section.
Designing Forecasting Questions
Once one has determined the total expected utility equation(s) relevant for the proposal(s) that they are trying to evaluate, the parameters of the equation(s) must be translated into forecasting questions for reviewers to respond to. In general, for each outcome, reviewers will need to answer the following four questions:
- If this proposal is funded, what is the probability that this outcome will occur?
- If this proposal is not funded, what is the probability that this outcome will still occur?
- What will be the scientific impact of this outcome occurring?
- What will be the social impact of this outcome occurring?
For the probability questions, one could alternatively ask reviewers about the different probability components (𝑃nature(𝑚𝑖), 𝑃proposal(𝑚𝑖), 𝑃other mechanism(𝑚𝑖), etc.), but in most cases it will be sufficient — and simpler for the reviewer — to focus on the top-level probabilities that feed into the TEU calculation.
In order for the above questions to tap into the benefits of the forecasting framework, they must be resolvable. Resolving the forecasting questions means that at a set time in the future, reviewers’ predictions will be compared to a ground truth based on the actual events that have occurred (i.e., was the outcome actually achieved and, if so, what was its actual impact?). Consequently, reviewers will need to be provided with the resolution date and the resolution criteria for their forecasts.
Resolution of the probability-based questions hinges mostly on a careful and objective definition of the potential outcomes, and is otherwise straightforward — though note that only one of the probability questions will be resolved, since they are mutually exclusive. The optimal resolution of the scientific and social impact questions may depend on the context of the project and the chosen approach to defining utility. A widely applicable approach is to resolve the utility forecasts by having either program managers or subject matter experts evaluate the results of the completed project and score its impact at the resolution date.
For our pilot, we asked forecasting questions only about the probability of success given funding (question 1 above) and the scientific and social impact of each outcome (questions 3 and 4); since we assumed that the probability of success without funding was zero, we did not ask question 2. Because outcomes for the FRO proposals were designed to be either independent or sequential, we did not have to ask additional questions on the joint probability of multiple outcomes being achieved. We chose to resolve our impact questions with a post-project panel of subject matter experts.
Additional Considerations
In general, there is a tradeoff in implementing this approach between simplicity and thoroughness, efficiency and accuracy. Here are some additional considerations on that tradeoff for those looking to use this approach:
- The responsibility of determining the range of potential outcomes for a proposal could be assigned to three different parties: the proposal author, the proposal reviewers, or the program manager. First, grantmakers could ask proposal authors to comprehensively define within their proposal the potential primary and secondary outcomes and/or project milestones. Alternatively, reviewers could be allowed to individually — or collectively — determine what they see as the full range of potential outcomes. The third option would be for program managers to define the potential outcomes based on each proposal, with or without input from proposal authors. In our pilot, we chose to use the third approach with input from proposal authors, since it simplified the process for reviewers and allowed us to limit the number of outcomes under consideration to a manageable amount.
- In many cases, a “failed” or null outcome may still provide meaningful value by informing other scientists that the research method doesn’t work or that the hypothesis is unlikely to be true. Considering the replication crises in multiple fields, this could be an important and unaddressed aspect of peer review. Grantmakers could choose to ask reviewers to consider the value of these null outcomes alongside other outcomes to obtain a more complete picture of the project’s utility. We chose not to address this consideration in our pilot for the sake of limiting the evaluation burden on reviewers.
- If grant recipients’ are permitted greater flexibility in their research agendas, this expected value approach could become more difficult to implement, since reviewers would have to consider a wider and more uncertain range of potential outcomes. This was not the case for our FRO Forecasting pilot, since FROs are designed to have specific and well-defined research goals.
Other Similar Efforts
Currently, forecasting is an approach rarely used in grantmaking. Open Philanthropy is the only grantmaking organization we know of that has publicized their use of internal forecasts about grant-related outcomes, though their forecasts do not directly influence funding decisions and are not specifically of expected value. Franzoni and Stephan are also currently piloting their Subjective Expected Utility approach with Novo Nordisk.
Conclusion
Our goal in publishing this methodology is for interested grantmakers to freely adapt it to their own needs and iterate upon our approach. We hope that this paper will help start a conversation in the science research and funding communities that leads to further experimentation. A follow up report will be published at the end of the FRO Forecasting pilot sharing the results and learnings from the project.
Acknowledgements
We’d like to thank Peter Mühlbacher, former research scientist at Metaculus, for his meticulous feedback as we developed this approach and for his guidance in designing resolvable forecasting questions. We’d also like to thank the rest of the Metaculus team for being open to our ideas and working with us on piloting this approach, the process of which has helped refine our ideas to their current state. Any mistakes here are of course our own.
We’ve created a tool to monitor the progress of federal actions on extreme heat, enhance accountability, and to allow stakeholders to stay informed on the evolving state of U.S. climate-change resilience.
By advocating for the integration of technology-focused green jobs within federal initiatives, there is an opportunity to broaden the talent pool and harness the potential of emerging technologies to tackle pressing environmental issues.
“We really wanted a range of perspectives – specifically from voices that have been traditionally left out of the conversation”
Understanding the implications of climate change in agriculture and forestry is crucial for our nation to forge ahead with effective strategies and outcomes.