Feasibility of a Low-Yield Gun-Type Terrorist Fission Bomb
Introduction
Edward Friedman and Roger Lewis’s essay “A Scenario for Jihadist Nuclear Revenge,” published in the Spring 2014 edition of the Public Interest Report, is a sobering reminder of both the possibility of a terrorist nuclear attack based on stolen highly-enriched uranium and the depressing level of public ignorance of such threats. Articles exploring the issue of terrorists or rogue sub-national actors acquiring and using a nuclear weapon or perpetrating some other type of nuclear-themed attack have a long history and have addressed a number of scenarios, including a full-scale program to produce a weapon from scratch, use of stolen reactor-grade plutonium, an attack with a radiological dispersal device, and the vulnerability of research reactors.[5]Equally vigorous are discussions of countermeasures such as detecting warheads and searching for neutron activity due to fissile materials hidden inside cargo containers. An excellent summary analysis of the prospects for a terrorist-built nuclear weapon was prepared almost three decades ago by Carson Mark, Theodore Taylor, Eugene Eyster, William Maraman and Jacob Wechsler, who laid out a daunting list of materials, equipment, expertise and material-processing operations that would be required to fabricate what the authors describe as a “crude” nuclear weapon – a gun or implosion-type device similar to Little Boy or Fat Man. The authors estimated that such a weapon might weigh on the order of a ton or more and have a yield of some 10 kilotons. Perpetrators would face a serious menu of radiological and toxicological hazards involved in processing fissile materials. For example, both uranium (U) and plutonium (Pu) are chemically toxic; also, U can ignite spontaneously in air and Pu tends to accumulate in bones and kidneys. Of course, longer-term health effects might be of little concern to a group of suicidal terrorists.
While the difficulties of such a project might provide reassurance that such an effort has a low probability of being brought to fruition, we might ask if nuclear-armed terrorists along the lines envisioned by Friedman and Lewis would be willing to settle for a relatively low-yield device to achieve their ends. A bomb with a yield of 10 percent of that of Little Boy would still create a devastating blast, leave behind a radiological mess, and generate no small amount of social and economic upheaval. Such a yield would be small change to professional weapons engineers, but the distinction between one kiloton and 15 kilotons might largely be lost on political figures and the public in the aftermath of such an event. Timothy McVeigh’s 1995 Oklahoma City truck bomb used about 2.5 tons of explosive; a one-kiloton detonation would represent some 400 such explosions and make a very powerful statement.
Motivated by Friedman and Lewis’s scenario, I consider the feasibility of an extremely crude gun-type U-235 device configured to be transported in a pickup truck or similar light vehicle. My concern is not with the difficulties perpetrators might face in acquiring fissile material and clandestinely preparing their device, but rather with the results they might achieve if they can do so. The results reported here are based on the basic physics of fission weapons as laid out in a series of pedagogical papers that I have published elsewhere. The essential configuration and expected yield of the device proposed is described in the following section; technical details of the physics computations are gathered in the Appendix.
A Crude Gun-Type Fission Bomb
The bare critical mass of pure U-235 is about 46 kg; this can be significantly lowered by provision of a surrounding tamper. I frame the design of a putative terrorist bomb by assuming that perpetrators have available 40 kg of pure U-235 to be packaged into a device with a length on the order of 2-3 meters and a total estimated weight of 450 kg (1000 pounds), of which 200 kg is budgeted for tamper material. The 40-kg core is subcritical, and the uranium need not be divided up into target and projectile pieces as in the Friedman-Lewis scenario, although the design suggested here could easily be modified to accommodate such an arrangement.
As sketched below, I assume that the uranium is formed into a cylindrical slug of diameter and length Lcore. The core and a plug of tamper material are to be propelled down an artillery tube into a cylindrical tamper case such that the core will be located in the middle of the case once assembly is complete; the assembled core-plus-tamper is assumed to be of diameter and length Ltamp. The choice of tamper material is a crucial consideration; it can seriously affect the predicted yield. In the case of Little Boy, readily-available tungsten-carbide (WC) was employed. Beryllium oxide (BeO) has more desirable neutron-reflective properties, but is expensive and its dust is carcinogenic; more importantly, an effort to acquire hundreds of kilograms of it is likely to bring unwanted attention. I report results for both WC and BeO tampers.
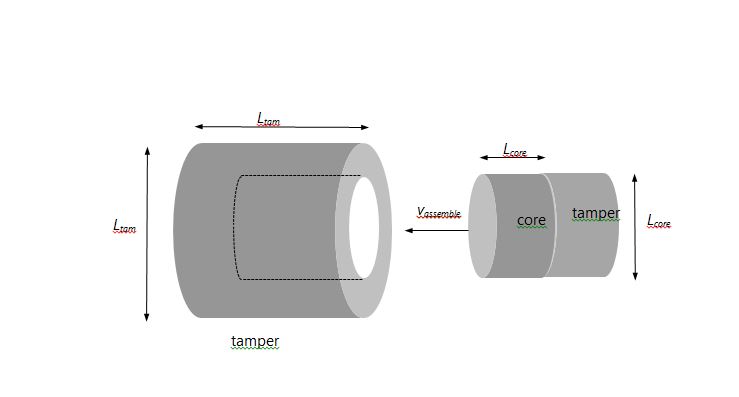
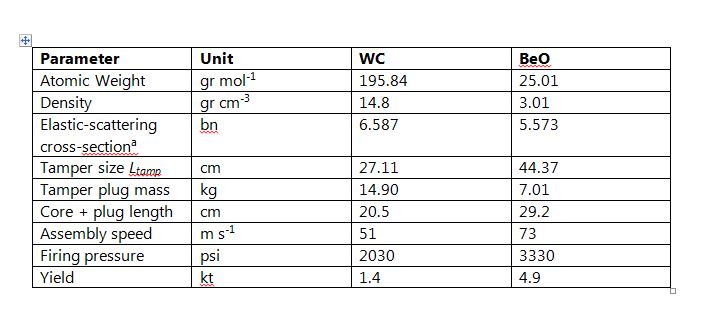
Adopted parameters and calculated results are gathered in Table 1. Technical details are described in the Appendix; the last line of the table gives estimated yields in kilotons. To estimate these yields I used a FORTRAN version of an algorithm which I developed to simulate the detonation of a spherical core-plus-tamper assembly (see the numerical simulation paper cited in footnote 10). A spherical assembly will no doubt give somewhat different results in detail from the cylindrical geometry envisioned here, but as the program returns an estimated yield for a simulation of Little Boy in good accord with the estimated actual yield of that device, we can have some confidence that the results given here should be sensible.
For both configurations in Table 1, the sum of the core, tamper, and artillery-tube masses is about 315 kg (700 lb). With allowance for a breech to close off the rear end of the tube, neutron initiators, detonator electronics, propelling chemical explosives and an enclosing case (which need not be robust if the weapon is not to be lifted), it appears entirely feasible to assemble the entire device with a total weight on the order of 1,000 pounds. Beryllium oxide is clearly preferable as the tamper material, but even with a tungsten-carbide tamper the yield is about 10 percent of that of Little Boy. In open terrain a 2-kiloton ground-burst creates a 5-psi overpressure out to a radius of about one-third of a mile; such an overpressure is quite sufficient to destroy wood-frame houses.
In summary, the sort of vehicle-deliverable makeshift gun-type fission weapon envisioned by Friedman and Lewis appears to be a very plausible prospect; yields on the order of a few kilotons are not out of reach. In view of the fact that all of the calculations in this paper are based on open information, there are sure to be nuances in the physics and particularly the engineering involved that would make realization of such a device more complex than is implied here. But this exercise nevertheless serves as a cautionary tale to emphasize the need for all nuclear powers to rigorously secure and guard their stockpiles of fissile material.
Technical Appendix
Refer to Table 1 and the figure above. A 40-kg U-235 core of normal density (18.71 gr cm-3) will have Lcore = 13.96 cm. The first three lines of Table 1 give adopted atomic weights, densities, and elastic-scattering cross sections for each tamper material. The next two lines give the tamper size and plug mass, and the sixth line the total length of the core-plus-plug bullet.
To estimate the yield of the proposed device I assumed for sake of simplicity that the core is spherical (radius ~ 8 cm) and surrounded by a snugly-fitting 200-kg tamper. Each fission was assumed to liberate 180 MeV of energy and secondary neutrons of average kinetic energy 2 MeV. The number of initiator neutrons was assumed to be 100, radiation pressure was assumed to dominate over gas pressure in the exploding core, and the average number of neutrons per fission was taken to be n = 2.637.
Lines 7 and 8 in Table 1 refer to two important considerations in bomb design: the speed with which the core seats into the tamper and the propellant pressure required to achieve this speed. The core material will inevitably contain some U-238, which, because of its high spontaneous fission rate (~ 7 per kg per second), means that there will be some probability for premature initiation of the chain reaction while the core and tamper are being assembled. (There is no danger of pre-detonation before seating as 40 kg is less than the “bare” critical mass of U-235. The danger during seating arises from the fact that the tamper lowers the critical mass.) The key to minimizing this probability lies in maximizing the assembly speed. If our 40-kg core contains 10 percent by mass U-238, the pre-detonation probability can be kept to under 10 percent if the time during which the core is in a supercritical state during assembly is held to no more than four milliseconds (see the pre-detonation paper cited in footnote 10). The seventh line of Table 1 shows corresponding assembly speeds based on this time constraint and the core-plug lengths in the preceding line. These speed demands are very gentle in comparison to the assembly speed employed in Little Boy, which was about 300 m s-1.
To achieve the assembly speed I assume that (as in Little Boy), the core-plus-plug is propelled along a tube by detonation of a conventional explosive adjacent to the rear end of the tamper plug in the tail of the weapon. To estimate the maximum pressure required, I assumed that the propulsion is provided by the adiabatic expansion (in which no heat is gained or lost) of the detonated explosive. Adiabatic expansion of gas to propel a projectile confined to a tube has been extensively studied; an expression appearing in Rohrbach et. al. can be used to estimate the initial pressure required given the cross-sectional area of the tube, the mass of the projectile, the length of the tube, a value for the adiabatic exponent _gand the assembly speed to be achieved. This pressure also depends on the initial volume of the detonated explosive; for this I adopted a value of 0.004 m3, about the volume of the core-plug assemblies. The eighth line of Table 1 shows the estimated necessary initial pressures (neglecting any friction between the projectile and the tube) for a travel length of 1.5 meters for g = 1.4; this value of g is characteristic of a diatomic gas. These pressures are very modest, and would set no undue demands on the tube material. Stainless steel, for example, has an ultimate strength of ~ 500 MPa (~75,000 psi); such a tube of inner diameter 7 cm, thickness 1 cm, and length 2 meters would have a mass of about 75 kg. This would bring the sum of the core, tamper, and tube masses to ~ 315 kg (700 lb).
A final technical consideration is the so-called fizzle yield that this makeshift weapon might achieve, that is, its yield if the chain reaction should begin at the moment when the core achieves first criticality. As described by von Hippel and Lyman in Mark (footnote 3), the fizzle yield as a fraction of the nominal design yield can be estimated from the expression Yfizzle/Ynominal ~ (2t F/a tO)3/2, where t is the average time that a neutron will travel before causing a fission, F is the natural logarithm of the number of fissions that have occurred when the nuclear chain reaction proper can be considered to have begun, a is a parameter in the exponential growth rate of the reaction set by the masses and sizes of the core and tamper, and tO is the time required to complete the core assembly. As described by Mark, t ~ 10-8 sec and F ~ 45. For the design posited here, a~ 0.32 for the WC tamper and ~ 0.47 for the BeO tamper; see Reed (2009) in footnote 10 or Sect. 2.3 of the last reference in footnote 10 regarding the computation of a. Taking tO = 0.004 sec gives Yfizzle/Ynominal ~ 1.9 x 10-5 for the WC tamper and 1.0 x 10-5 for the BeO tamper. With nominal yields of 1.4 and 4.9 kt, the estimated fizzle yields are only ~ 27 and 50 kilograms equivalent. While the perpetrators of such a device might be willing risk such a low yield in view of the low pre-detonation probability involved, they would be well-advised to increase the assembly speed as much as possible.
*Fission-spectrum averaged elastic-scattering cross-sections adopted from Korea Atomic Energy Research Institute Table of Nuclides, http://atom.kaeri.re.kr
Edward A. Friedman & Roger K. Lewis, “A Scenario for Jihadist Nuclear Revenge,” Federation of American Scientists Public Interest Report 67 (2) (Spring 2014).
Robert Harney, Gerald Brown, Matthew Carlyle, Eric Skroch & Kevin Wood, “Anatomy of a Project to Produce a First Nuclear Weapon,” Science and Global Security 14 (2006): 2-3, 163-182.
J. Carson Mark, “Explosive Properties of Reactor-Grade Plutonium,” Science and Global Security 4 (1993): 1, 111-128.
J. Magill, D. Hamilton, K. Lützenkirchen, M. Tufan, G. Tamborini, W. Wagner, V. Berthou & A. von Zweidorf, “Consequences of a Radiological Dispersal Event with Nuclear and Radioactive Sources,” Science and Global Security 15 (2007): 2, 107-132.
Steve Fetter, Valery A. Frolov, Marvin Miller, Robert Mozley, Oleg F. Prilutsky, Stanislav N. Rodinov & Roald Z. Sagdeev, “Detecting nuclear warheads,” Science and Global Security 1 (1990): 3-4, 225-253.
J. I. Katz, “Detection of Neutron Sources in Cargo Containers,” Science and Global Security 14 (2006): 2-3, 145-149.
J. Carson Mark, Theodore Taylor, Eugene Eyster, William Maraman & Jacob Wechsler, “Can Terrorists Build Nuclear Weapons?” Paper Prepared for the International Task Force on the Prevention of Nuclear Terrorism. Nuclear Control Institute, Washington, DC (1986). Available at http://www.nci.org/k-m/makeab.htm
Cristoph Wirz & Emmanuel Egger, “Use of nuclear and radiological weapons by terrorists?” International Review of the Red Cross 87 (2005): 859, 497-510.
B. Cameron Reed, “Arthur Compton’s 1941 Report on explosive fission of U-235: A look at the physics.” American Journal of Physics 75 (2007): 12, 1065-1072; “A brief primer on tamped fission-bomb cores.” American Journal of Physics 77 (2009): 8, 730-733; “Predetonation probability of a fission-bomb core.” American Journal of Physics 78 (2010): 8, 804-808; “Student-level numerical simulation of conditions inside an exploding fission-bomb core.” Natural Science 2 (2010): 3, 139-144; “Fission fizzles: Estimating the yield of a predetonated nuclear weapon.” American Journal of Physics, 79 (2011): 7, 769-773; The Physics of the Manhattan Project (Heidelberg, Springer-Verlag, 2010).
Z. J. Rohrbach, T. R. Buresh & M. J. Madsen, “Modeling the exit velocity of a compressed air cannon,” American Journal of Physics 80 (2012): 1, 24-26.
Cameron Reed is the Charles A. Dana Professor of Physics at Alma College, where he teaches courses ranging from first-year algebra-based mechanics to senior-level quantum mechanics. He received his Ph.D. in Physics from the University of Waterloo (Canada). His research has included both optical photometry of intrinsically bright stars in our Milky Way galaxy, and the history of the Manhattan Project. His book The History and Science of the Manhattan Project was recently published by Springer.
The United Kingdom is modernizing its stockpile of nuclear weapons and delivery systems, as detailed today in the Federation of American Scientists latest edition of its Nuclear Notebook, “United Kingdom Nuclear Forces, 2024”.
FAS believes the resolution is a necessary advancement of scientific understanding of the devastating consequences of a nuclear war.
The U.S. should continue its voluntary moratorium on explosive nuclear weapons tests and implement further checks on the president’s ability to call for a resumption of nuclear testing.
To help protect U.S. critical infrastructure workers, the next presidential administration should ensure ample supplies of high-quality respiratory personal protective equipment.