
 Introduction to
Naval Weapons Engineering
Introduction to
Naval Weapons Engineering
As opposed to pulsed
radar systems, continuous wave (CW) radar systems emit electromagnetic
radiation at all times. Conventional CW radar cannot measure
range because there is no basis for the measurement of the
time delay. Recall that the basic radar system created pulses
and used the time interval between transmission and reception
to determine the target's range. If the energy is transmitted
continuously then this will not be possible.
CW radar can measure
the instantaneous rate-of-change in the target's range.
This is accomplished by a direct measurement of the Doppler
shift of the returned signal. The Doppler shift is a
change in the frequency of the electromagnetic wave caused by
motion of the transmitter, target or both. For example, if the
transmitter is moving, the wavelength is reduced by a fraction
proportional to the speed it is moving in the direction of propagation.
Since the speed of propagation is a constant, the frequency must
increase as the wavelength shortens. The net result is an
upwards shift in the transmitted frequency, called the Doppler
shift.

Figure 1. Doppler shift from moving transmitter
Likewise, if the receiver is moving opposite to the direction of propagation, there will a increase in the received frequency. Furthermore, a radar target which is moving will act as both a receiver and transmitter, with a resulting Doppler shift for each. The two effects caused by the motion of the transmitter/receiver and target can be combined into a net shift the frequency. The amount of shift will depend of the combined speed of the transmitter/receiver and the target along the line between them, called the line-of-sight (LOS).
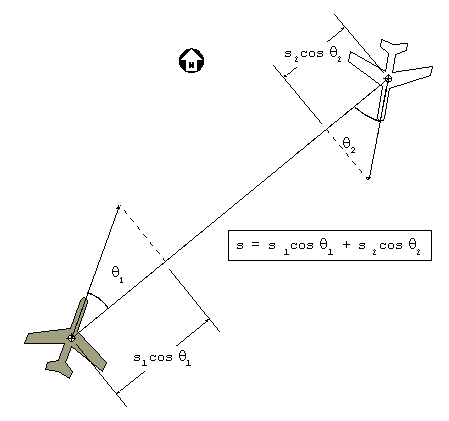
Figure 2. Calculating the relative speed in the line-of-sight.
The Doppler shift can be calculated with knowledge of the transmitter/receiver and target speeds, here designated as s1 and s2 respectively, and the angles between their direction of motion and the line-if-sight, designated q1 and q2. The combined speed in the line-of-sight is
s = s1 cosq1 + s2 cosq2 .
This speed can also be interpreted as the instantaneous rate of change in the range, or range rate. As long as the problem is confined to two-dimensions, the angles also have simple interpretations: q1 = the relative bearing to the target. The difference between the course of the transmitter/receiver and the true bearing to the target. This follows the old nautical rule:
Relative Bearing = True Bearing - Heading
Due to the characteristics of the cosine function, it makes no difference whether angle is positive or negative (strictly speaking, relative bearings are always positive and range from 0 to 3590). q2 = the target angle (relative bearing of transmitter/receiver from target). Computed in an identical manner as the relative bearing, except that the target's course is substituted for the heading and the reciprocal bearing is used instead of the true bearing to the target. The reciprocal bearing is found by:
Reciprocal Bearing = True Bearing 1800
Again, it does not matter is this result is positive, negative or even beyond 3600, although the proper result would be in the range of 0-3590. Assuming that the range rate is known the shift in returned frequency is
Df = 2s/l
where l is the wavelength of
the original signal. As an example, the Doppler shift
in an X-band (10 GHz) CW radar will be about 30 Hz for every 1
mph combined speed in the line-of-sight.
Example: speed gun.
Police often use CW
radar to measure the speed of cars. What is actually measured
is the fraction of the total speed which is towards the radar.
If there is some difference between the direction of motion and
the line-of-sight, there will be error. Fortunately for
speeders, the measured speed is always lower than the actual.
CW radar systems are
used in military applications where the measuring the range
rate is desired. Of course, range rate can be determined
from the basic pulsed radar system by measuring the change in
the detected range from pulse to pulse. CW systems
measure the instantaneous range rate, and maintain continuous
contact with the target.
It is also possible
to use a CW radar system to measure range instead of range rate
by frequency modulation, the systematic variation of the transmitted
frequency. What this does in effect is to put a unique "time
stamp" on the transmitted wave at every instant. By
measuring the frequency of the return signal, the time delay between
transmission and reception can be measure and therefore the range
determined as before. Of course, the amount of frequency
modulation must be significantly greater than the expected Doppler
shift or the results will be affected.
The simplest way to
modulate the wave is to linearly increase the frequency.
In other words, the transmitted frequency will change at a constant
rate.

Figure 3. FMCW theory of operation.
The FMCW system measures the instantaneous difference between the transmitted and received frequencies, Df. This difference is directly proportional to the time delay, Dt, which is takes the radar signal to reach the target and return. From this the range can be found using the usual formula, R = cDt/2. The time delay can be found as follows:
Dt = T Df/(f2-f1) where:
f2 = maximum frequency
f1 = minimum frequency
T = period of sweep from f1 to f2,
and Df = the difference between transmitted
and received.
There is a slight problem which occurs when the sweep resets the
frequency and the frequency difference becomes negative (as shown
in the plot of Df vs. time). The system
uses a discriminator to clip off the negative signal, leaving
only the positive part, which is directly proportional to the
range. Here is a system diagram: 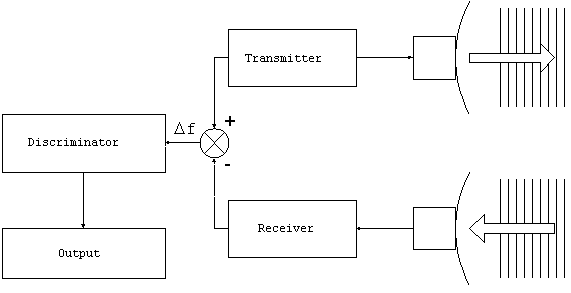
Combining these equations into a single form for the range
R = 2cTDf/(f2 - f1)
where Df is the difference between
the transmitted and received frequency (when both are from the
same sweep, i.e. when it is positive).
Another
way to construct a FMCW system, is to compare the phase difference
between the transmitted and received signals after they have been
demodulated to receiver the sweep information. This system
does not have to discriminate the negative values of Df.
In either case however, the maximum unambiguous range will still
be determined by the period, namely
Runamb = cT/2
FMCW systems are often used for radar altimeters, or in radar
proximity fuzes for warheads. These systems do not have a minimum
range like a pulsed system. However, they are not suitable for
long range detection, because the continuous power level they
transmit at must be considerably lower than the peak power of
a pulsed system. You may recall that the peak and average power
in a pulse system were related by the duty cycle,
Pave = DC *Ppeak
For a continuous wave system, the duty cycle is one, or alternatively, the peak power is the same as the average power. In pulsed systems the peak power is many times greater than the average.