

Page
1–1. Units of Measurement
001. Fundamental quantities of measurement
002. Systems of measurement
003. The measure of temperature
1–2. Motion
004. The quantities of motion and computing their elements
005. The force of gravity
006. Laws of motion
007. Circular motion and the forces involved
1–3. Properties of the Atmosphere
008. Measures of atmospheric substance
009. Measures of moisture in the atmosphere
1–4. Gas Laws, Heat Transfer, and Changes of State
010. The gas laws
011. How atmospheric gases change temperature
012. The quantity heat
013. Heat transfer
014. States of matter
1–5. Cloud Physics
015. Cloud microphysics
016. Cloud dynamics
HYSICS is the science of matter and energy. It is primarily concerned with the laws and properties of the material universe. Our understanding of these laws and properties has been the basis for many of the advancements made in the areas of mechanics, heat, sound, and electricity. Ultimately, the study of physics has led us into a completely new age, the nuclear age.
The use of physics is not limited to physicists. To an ever increasing extent, our expanding knowledge of matter is being applied to all areas of science, including the science of meteorology.
The majority of what we know about the atmosphere has come from the study of physics. Therefore, it is essential for every meteorologist to have an understanding of basic physics. This understanding not only will make your job as a weather journeyman more meaningful but will prepare you to advance in this highly specialized scientific field.
In understanding the basics of physics, we have to understand how to measure different quantities associated with this science. These quantities are expressed in terms common people do not use every day. It’s important to understand what these quantities represent and how they are measured before you understand their application. Let’s begin by exploring some fundamental measurements used in the study of physics.
001. Fundamental quantities of measurement
Physical quantities must be expressed as some measure. Surprisingly enough, we can express all quantities by using one or more of the three fundamental quantities of measurement—length, mass, and time.
Length
We can describe length as the size of an object in one plane—a linear measure. By linear, we mean in relation to length only. For example, if someone asks you how long a particular object is, a single dimension should come to mind—the distance from one end of the object to the other. If you are asked what the object’s width is, again a single dimension comes to mind—the distance between the sides of the object. Therefore, we can define length as a one-dimensional measure of distance. Two frequently used quantities of measurement are derived from the fundamental quantity of length—area and volume.
Area
Area is the measure of an object’s surface using length in two dimensions—length and width. To determine the area of an object, multiply the length by the width and label the result in square units. Consider a rectangle that measures 6 units long and 3 units wide. To compute its surface area, multiply its length times its width and express the answer as 18 square units. If you draw lines inside the rectangle, each unit apart and parallel to the sides, the rectangle is divided into 18 square units, as shown in figure 1–1.
There are different formulas for determining surface areas for different shaped objects. For example, to compute the area of a circle, multiply p times the square of the radius. The symbol p (read pi) equates to approximately 3.1416 and is the ratio of the circumference of any circle to its diameter. We express the surface area of a circle in square units.
Special abbreviations have been adopted to represent areas in formulas. These abbreviations can take one of two forms. One form is a combination of the abbreviation for square (sq) and the abbreviation for the unit of measurement. For example, square inch is represented as sq in, square foot is sq ft, and so on. The second method is to use the exponent 2 on the abbreviation for the unit of measure. For example a square centimeter is then expressed as "cm2;" a square mile as "mi2." The table below contains a list of measures of length and their abbreviations that you can use in the manner described above.
|
Inch = in |
Millimeter = mm |
|
Foot = ft |
Centimeter = cm |
|
Yard = yd |
Meter = m |
|
Mile = mi |
Kilometer = km |
Volume
Volume is the measure of an object using length in three dimensions—length, width, and depth. To compute the volume of an object, take the product of the three dimensions and express it in cubic units. Consider a box that is 6 units long, 3 units wide, and 2 units deep. This box occupies a 3-dimensional space—it has volume. To determine how much volume the box has, multiply the three dimensions (i.e., 6 × 3 × 2 = 36). Therefore, the box has 36 cubic units of volume. If we cut through each dimension of the box in widths equal to 1 unit, the result looks like figure 1–2. Notice there are 36 little boxes, each measuring 1 unit by 1 unit by 1 unit, or 1 cubic unit.
As in the measure of area, we use standard abbreviations to represent cubic measure. We can represent cubic measure by preceding the unit of measure with the abbreviation "cu", as in "cu ft," or by adding the exponent "3" to the unit of measure, as in "ft3."
Mass
This fundamental quantity of measurement is one that usually confuses many people. Perhaps this comes from our use of terms such as massive. For example, if someone describes an object to you as massive, or someone says, "This object really has some mass," something very large and heavy probably comes to mind. Mass is not the measure of an object’s size or weight, but the measure of the quantity of matter in an object. Suppose you have a solid rubber ball—this ball contains a definite quantity of matter, here rubber.
The important property of mass is that it is unaffected by its environment. In the example of the rubber ball, squeezing it may reduce its size, but not its matter; if we fly the ball to the Moon, we reduce its weight but its matter remains unchanged. Only by adding or removing matter can we change the mass of an object.
Do not confuse mass with weight, though we express their measures in the same terms. Weight is the combination of mass and the effects of gravity, while mass is unaffected by gravity. We usually express the mass of a body in grams. For example, one cubic centimeter of distilled water at a temperature of 4 degrees Celsius (4°C) has a mass of 1 gram. Knowing this, you could use a balance scale to determine the mass of any object. For example, to find the mass of a cubic centimeter of iron, you could compare it to several cubic centimeters of distilled water. If the scale balances with 10 cubic centimeters of water placed opposite the iron, the iron’s mass is 10 grams.
Time
Time is the third fundamental quantity of measurement. To most of us, time means a certain hour of the day, such as the time we go to work, when our favorite show is on TV, etc. In science, time is frequently a measure of the duration of an event or how long it takes for something to happen. We use time to express relationships with other events.
Before you can measure a quantity, such as distance, you must have a standard to use as the basis for the measurement. Imagine the frustration of early man in trying to tell a friend how far to walk to get to a newly discovered location or how long there would be daylight. Problems like these probably led to the development of standards or units to describe such quantities.
A complete set of units for all kinds of quantities is called a system of units. Several systems have been devised and are in use today. Each system is named for the units by which it measures the fundamental quantities. The two most frequently used systems are the British and the International systems.
British system of measurement
The British system, commonly used in the United States, was adopted from the British. The units of measure—the foot, the pound, and the second—are the basis for the system that scientists call the foot, pound, and second (FPS) system of measurement.
In the FPS system the basic unit for each fundamental quantity is as follows:
Although this system is still readily used by United States citizens, a switch to a metric system is inevitable. Most of the rest of the world uses metric systems and our country has been slowly incorporating the metric system into the public. Let’s now discuss a metric system that is used in the atmospheric science area.
The International system of measurement
Officially called the Systeme International (SI), units are used throughout the world as the standard system. The portion of this system dealing with our (the weather field’s) three fundamental quantities (mass, length, and time) is called the Meter Kilogram Second (MKS) system (Tipler, 1976). Fundamental units give a standard against which we can measure the fundamental quantities.
In the MKS system the fundamental unit for each fundamental quantity is as follows:
In the study of atmospheric sciences, weather journeymen use a base unit derived from the MKS system. The following are base units of the MKS system:
Notice that the only difference from the fundamental unit of the MKS system to the base unit was a change of the measurement for mass. We in the weather field use the gram as a base unit because it’s the unit required to calculate atmospheric formulas. Also notice that the second is the unit of measure for time in both systems. Internationally, there is only one standard for measuring time—the second.
MKS unit prefixes
In the MKS system, we use unit prefixes to distinguish between very large and very small values of fundamental quantities. We place the prefixes ahead of the base unit (grams, meters or seconds). This allows us to express magnitudes in smaller numbers (i.e., 100 kilometers instead of 100,000 meters). Use the following table to convert different magnitudes:
|
MKS unit / prefix |
Number of base units |
Exponential value |
|
kilo / (k) |
1000 |
103 |
|
hecto / (h) |
100 |
102 |
|
deca / (da) |
10 |
101 |
|
Base unit (gram, meter, second) |
1 |
100 |
|
deci / (d) |
0.1 |
10–1 |
|
centi / (c) |
0.01 |
10–2 |
|
milli / (m) |
0.001 |
10–3 |
|
micro / (m ) |
0.000001 |
10–6 |
Unit conversions (large to small)
Let’s begin now by converting from a large prefix to a smaller prefix by use of the table listed above.
Example: 540 dam to dm.
Unit conversions (small to large)
Let’s now convert a small prefix to a larger prefix. For example: convert 5400 m to dam.

Notice that when we converted from a large prefix to a smaller prefix we moved down in the table. Our exponent was the number of spaces moved and it was positive. Conversely, when we converted from a small prefix to a larger prefix, we moved up in the table. Our exponent was again the number of spaces moved but the exponent was negative. We need an understanding of the MKS system and how to convert for different units of measure for evaluating equations in physics.
003. The measure of temperature
Temperature is another important measure in the study of physics. Although most definitions of temperature are usable, some are much better than others. For example, we may define temperature as a measure of how hot or cold an object is. This is definitely a true statement, but it is somewhat vague for use in physics. A better definition is the one used by the scientific community: temperature is the measure of molecular activity of a body or object.
Figure 1–3. Hot and cold bodies.
We can illustrate molecular activity by comparing two like bodies at different temperatures, one relatively hot compared to the other (fig. 1–3). Notice that in the colder body, object A, the molecules represented by shivering figures are somewhat motionless. The molecules of object B, represented by jumping figures, possess more thermal energy. As molecules move about, they collide with one another. These collisions produce sensible energy—heat. Temperature is a measure of this energy; the more collisions that occur, the higher is the object’s temperature.
Thermal energy is transferred between objects in one direction—warm to cold. That is, a warm body naturally transfers some of its thermal energy to a colder body. For example, of the two objects in figure 1–3, object B may transfer some of its energy to object A until the molecules of both objects have an equal amount of thermal energy—that is, until their temperatures are the same. When ice cubes cool a drink, the heat of the drink is transferred to the colder ice cubes This is another example of thermal energy being transferred from warm to cold.
The scales we use to measure temperature
Although there are many temperature scales, in meteorology you need only be concerned with three—Celsius, Fahrenheit, and Kelvin (absolute scale). To compare the three scales, we must define two fixed temperatures and a scale difference between them. The two fixed temperatures are the freezing and boiling temperatures of water. Compare the freezing and boiling points of each scale shown below:
|
Scale |
Freezing Point |
Boiling Point |
|
Fahrenheit |
32° |
212° |
|
Celsius |
0° |
100° |
|
Kelvin |
273° |
373° |
Notice that the Fahrenheit scale has 180 degrees between freezing and boiling; in the other two, there are only 100 degrees.
Conversion of temperature scales
The use of three different temperature scales requires you to know how to convert from one scale to another. There are even times when you must report observed temperatures in two different scales.
Fahrenheit-Celsius conversions
Recall that the Fahrenheit scale has 180 degrees between freezing and boiling, while the Celsius scale has 100 degrees. Therefore, 1.8 degrees on the Fahrenheit scale equals 1 degree on the Celsius scale. Also remember that the different values for the freezing point are 32 degrees Fahrenheit (32°F) and 0 degree Celsius (0°C). Therefore, to convert Celsius to Fahrenheit, multiply the Celsius temperature by 1.8 and add to 32. The formula for this conversion is: F = 1.8C + 32. Now let’s test the formula to see if 0°C will convert to 32°F.
F = 1.8C + 32
F = 1.8(0) + 32
F = 0 + 32
F = 32°
We can use the same formula to convert from Fahrenheit to Celsius. This is shown below by converting 32°F to its Celsius equivalent:
32 = 1.8(C) + 32
32 – 32 = 1.8(C) + 32 – 32
0 = 1.8(C)
![]()
![]()
0° = C
Kelvin conversions
Conversion to the Kelvin scale is a simple process. Just like the Celsius scale, the Kelvin scale has 100 divisions between freezing and boiling. Therefore, since the Kelvin reading for freezing is 273 and the Celsius reading is 0, you can convert from Celsius to Kelvin (K) by adding 273 to the Celsius reading: K = C + 273. Conversion from Kelvin to Celsius is just the reverse or: C = K – 273. When you need conversions between Kelvin and Fahrenheit, use the conversion to Celsius as an intermediate step.
Self–Test Questions
After you complete these questions, you may check your answers at the end of the unit.
001. Fundamental quantities of measurement
Define the fundamental quantity of measure that is described by each of the following statements:
1. The amount of matter in an object.
2. The distance between two points.
3. Expresses relationships with other events.
4. Only a change in matter will change this measure.
5. Match the abbreviated forms of measurements in column B with the measurements in column A. Column B items may be used more than once or not at all.
Column A |
Column B |
____1. Square centimeter. ____2. Cubic centimeter. ____3. Square mile. ____4. Cubic meter. ____5. Square meter. ____6. Square inch. ____7. Cubic millimeter. ____8. Square kilometer. |
a. cu m. b. cm2. c. sq in. d. cm3. e. mm3. f. m2. g. in2. h. cu mm. i. sq cm. j. cu cm. k. mi2. l. m3. m. sq mi. n. sq m. o. sq km. p. km2. |
002. Systems of measurement
1. Determine which fundamental quantity of measurement is expressed in the following units of measure and to which system of measurement the units belong:
a. Gram.
b. Foot.
c. Second.
d. Pound.
e. Meter.
2. Fill in the missing values in the table below:
|
MKS unit / prefix |
Number of base units |
|
1000 |
|
|
hecto / (h) |
100 |
|
deca / (da) |
|
|
Base unit (gram, meter, second) |
|
|
0.1 |
|
|
centi / (c) |
0.01 |
|
0.001 |
|
|
micro / (m ) |
003. The measure of temperature
1. Explain the relationship between temperature and molecular activity in an object?
2. Determine what happens to thermal energy between two objects of different temperature.
3. What are the three temperature scales we primarily use in meteorology? Define the freezing and boiling point for each.
4. Perform the following temperature conversions.
a. 45°F to degrees Celsius.
b. 24°C to degrees Fahrenheit.
c. 30°C to degrees Kelvin.
d. 425°K to degrees Fahrenheit.
Motion is the action or process of changing positions or the process of moving from one point to another. The motion or movement of the atmosphere is very important to your eventual understanding of the science of meteorology. The same laws that govern the motion of objects also govern the motion of the atmosphere. In this section, we discuss the various elements of motion and the laws governing these quantities.
004. The quantities of motion and computing their elements
The quantities of motion are those physical quantities that are important to the measure of how things move. These measures also are fundamental to understanding the laws of motion we discuss later in this section. For our purposes, we discuss four elements of motion:
Speed
Any object in motion has speed—a flying plane, a moving train, and a person walking down the street all have speed. In physics, speed is the rate of motion of an object and is represented by the letter S. Speed or rate of motion is the ratio of distance (d) to time (t) or a measure of length per unit of time.
The formula for determining speed or rate is:
S = ![]()
For example, if you drive your car 360 miles in 6 hours, you can compute the rate by substituting the values for distance and time into the formula:
S = ![]()
Since rate is expressed as distance per unit time, you must change 6 hours to a single unit or 1 hour; therefore:
S = ![]() =
= ![]()
The common expression for this is 60 miles per hour, or 60 mph.
We use many different units to express speed; for example, nautical miles per hour (knots), feet per second (fps), and meters per second (mps) are often used.
Velocity
Velocity is another expression of speed, but the two terms are not interchangeable. Velocity is speed in a specific direction, but speed itself does not account for direction. For example, an aircraft flying 90° at 350 knots (kts) has a direction of 90° and a speed of 350 knots; its velocity is 350 knots toward 90°. Velocity is vector quantity because it has both magnitude and direction.
Acceleration
When most people think of acceleration, they think of "speeding up" in a car. In physics, acceleration is the change in rate per unit time. To compute acceleration, you must know the change in rate and the time it took to make the change. Look at the formula for acceleration, where "a" represents acceleration:
a = ![]()
Note S1 is the beginning rate and S2 is the rate after acceleration ceases; therefore, S2 – S1 is the change in rate.
Suppose you were shopping for a new sports car and narrowed your choice to one of two models, A or B. You want the one having the best acceleration, but the acceleration for car A is 0 to 60 in 8.2 seconds; car B’s acceleration is 0 to 50 in 6.9 seconds. It might seem like a tough choice, but you could use the formula for acceleration to help. Follow along as we solve for car A and B.
Car A:
a = ![]()
a = ![]()
a = ![]()
Car B:
a = ![]()
a = ![]()
a = ![]()
With each car’s acceleration expressed as a change in rate per unit time, you could make the right choice, car A.
In physics, acceleration is most often expressed as change in rate expressed in units of distance per second per second. For example, a change in rate of 1 centimeter per second with the time for the change being one second  Therefore, if an object changes it speed by 1 centimeter per second in one second, its acceleration is
Therefore, if an object changes it speed by 1 centimeter per second in one second, its acceleration is![]() . This also may be expressed as
. This also may be expressed as ![]() shown mathematically as:
shown mathematically as:
![]() =
= ![]() =
= ![]() or 1 cm per sec2
or 1 cm per sec2
Another definition of acceleration is a change in velocity. Since velocity has both magnitude and direction, we consider a change in either to be acceleration. In other words, a change in speed is acceleration and a change in direction is also acceleration. This will become more important when we discuss circular motions later.
Force
Force is a quantity derived from the quantities of mass and acceleration. Whenever a force acts on a body, an acceleration is produced in the direction of the force. This acceleration is directly proportional to the force applied and inversely proportional to the mass of body. For example, if you push against a chair with a force, the chair will move; how far the chair moves depends on how hard you push and the mass of the chair. To compute force, use the formula:
F = ma
where:
F = Force.
m = Mass.
a = Acceleration.
The dyne is the unit of force in the metric system. By definition, 1 dyne is the force required to accelerate 1 gram of matter at ![]() . So, if an object with a mass of 1 gram accelerates from a stationary state to 1 cm per second in a period of 1 second, a force of 1 dyne is acting on the object. Therefore, to compute force in dynes, we must express mass in grams and acceleration in
. So, if an object with a mass of 1 gram accelerates from a stationary state to 1 cm per second in a period of 1 second, a force of 1 dyne is acting on the object. Therefore, to compute force in dynes, we must express mass in grams and acceleration in ![]() . The example below shows the use of the formula to compute the force needed to accelerate 100 grams by 50 cm per sec2:
. The example below shows the use of the formula to compute the force needed to accelerate 100 grams by 50 cm per sec2:
F = 100 gm (50 cm per sec2)
F = 5,000 dynes
As you can see, the process is simple if the units are grams, centimeters, and seconds. Now let’s try a computation using different units, as in the force needed to accelerate 2 kilograms at 5 meters per hour per sec.
2 kilograms = 2,000 grams.
5 meters per hour = ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]() =
= ![]() .
.
![]()
 =
= ![]() .
.
F = (2,000 gm)![]()
F = 280 dynes
Gravity is the force that attracts one body to another. It is the force keeping you in your chair and your chair on the floor right now. When you think of this force, you probably think in terms of the Earth’s gravitational pull keeping you in your chair. This is only about a third of the story because gravity is a universal force. According to the universal law of gravitation, every body in the universe attracts every other body in the universe. Therefore, the force keeping you in your chair is a combination of the force attracting you and your chair, your chair and the floor, and you and the floor. As silly as it may sound, it is true your chair, the floor, even you are exerting gravitational force. Of course not everything attracts other objects equally.
The second part of the universal law states—the force attracting two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centers of their masses. In other words, the amount of gravitational attraction exerted by you or your chair is pretty small compared to that of the Earth.
The formula for universal gravitation is as follows:
F = G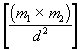
where:
F = Force in dynes.
G = gravitational constant.
m1 = Mass of one object.
m2 = Mass of the other object.
d = the distance separating the objects.
You can see that, despite the value of G, an increase in the mass of either object increases the force attracting them; an increase in the distance separating the objects reduces the force between them.
Acceleration due to gravity
Often referred to as uniformly accelerated motion, this is the acceleration of a free falling object due to the forces of gravity. You know if you drop a stone from some height, it falls to Earth, accelerating as it falls. We normally express this acceleration as centimeters per sec2 and represent it by the symbol "g."
Acceleration due to gravity depends on the force of gravity which is dependent on the distance between the centers of two masses. Acceleration due to gravity is different at all places on the Earth; it varies both with elevation and latitude. As elevation changes, the distance between the centers of mass changes. In the table below, notice the value for g is less at the locations with the higher elevation:
|
PLACE |
ELEVATION ABOVE SEA LEVEL IN METERS |
g (cm/sec2) |
|
Washington, DC |
103 |
980.095 |
|
St. Louis, MO |
154 |
980.001 |
|
Denver, CO |
1638 |
979.609 |
|
Pikes Peak, CO |
4293 |
978.954 |
NOTE: Each of these locations has roughly the same latitude (38°N).
As we stated before, g also varies with latitude—it is greatest at the poles and least at the equator. To see why, look at the cross section of the Earth in figure 1–4. Notice the differences in distance to the center of the Earth as measured from the Equator and as measured from the North Pole. If you were standing at the North Pole, you would be some 31,000 meters closer to the center of the mass of the Earth. By the formula for gravity, as distance between the centers of masses decreases, the force of gravity increases. This explains why, at sea level, g equals 978.039![]() at the Equator and 983.217
at the Equator and 983.217![]() at the North Pole. At 45°
latitude at sea level, g has a value of 980.621
at the North Pole. At 45°
latitude at sea level, g has a value of 980.621![]() . This is the value we normally use in physics to represent standard uniform acceleration.
. This is the value we normally use in physics to represent standard uniform acceleration.
Force caused by the acceleration due to gravity
From our previous discussion on acceleration, you probably think that, in order for an object to be accelerating, it must be in motion. In one sense this is true, but consider a stationary object on the Earth’s surface. This object is made of matter and, therefore, has mass. Though this object is stationary, it exerts a certain amount of force, but the formula for force is mass times acceleration. If the object isn’t moving anywhere, it is exerting force because of the effect of acceleration due to gravity. For example, if you push a paperweight off the table, it accelerates at a rate equal to g. Therefore, the paperweight is exerting a force equal to its mass times g or in this case F = m × g, where g represents acceleration. This force is important not only because of the effect it has on the motion of objects but because of the pressure exerted by objects.
We define a law as the result of defining certain quantities and relationships and then develop logical conclusions from those relationships. Thus far, we have defined the quantity motion and determined ways to measure the quantity. You have also learned that there are forces such as gravity that can either impede or create motion. For example, if you hold an object at arm’s length, you know that a force is exerted; if you release the object, it falls at an ever-increasing rate. Do we really know what causes and maintains motion? Sir Isaac Newton formulated three laws to explain the "whys" of motion.
Newton’s first law
Newton’s first law states that a body at rest remains at rest or a body in motion remains in motion unless it is acted on by an external force. For example, a smooth flat object placed on a smooth, flat surface of ice will stay where it is originally placed unless something pushes it. If the object is given a push, it will tend to move until something stops it. Additionally, the object will tend to move in one direction. You could say that objects tend to resist changes in their present state of motion.
Resistance to changes in motion was Galileo’s definition of inertia. Every body possesses inertia and some possess more than others; the amount depends on the mass of the body. Consider how easily you could move a cubic meter of styrofoam and how difficult it would be for you to move a cubic meter of lead. Consider both materials in motion. Which would be more difficult to stop or even make change directions? You could most likely reach out and touch the styrofoam to make it stop, but you probably couldn’t stop the lead object without risk of personal injury.
Newton’s second law
Observations in everyday life make it obvious that objects do not stay in a single state of motion forever. That is, bodies at rest eventually move; bodies in motion don’t always travel in a straight line and eventually come to rest. This describes accelerated motion, which is the result of one or more forces acting on a body. It is Newton’s second law that explains the relationship between acceleration, force, and inertia. His law states: "The acceleration of a body is directly proportional to the sum of forces acting on the body, inversely proportional to the mass of the body, and is in the direction of the sum of forces."
To move a block along a table top, you could push the block and cause it to accelerate along the surface of the table in the direction in which you are pushing. Newton also stated that acceleration is proportional to force; therefore, the harder you push, the more the block accelerates. The law also states that acceleration is inversely proportional to the mass; if the block is made of wood, it accelerates more than if it is made of steel.
In the above examples, we talked only about a single force acting on an object, but Newton’s law talked about a sum of forces. Suppose you and another person both push against the same side of a block. The block will accelerate at a rate equal to the sum of both forces. Since both forces are in the same direction, the block will move in that direction. What if you push on one side and the other person pushes on an adjacent side of the block—in what direction will the block move? Newton’s law said it will move in the direction of the sum of the forces. Since force has direction and magnitude, we can use vectors to solve this problem as shown in figure 1–5. The arrows labeled F1 and F2 represent the vectors of force; the arrow labeled "a" represents the resultant vector. Notice that the resultant vector is in a direction halfway between and has a length slightly longer than the force vectors.
Newton’s third law
In the simplest sense, we can define force as a push or a pull. Yet, Newton said that force is an interaction of two bodies. In other words, if you pull on a cart, the cart accelerates; if you hit a nail with a hammer, the nail penetrates the wood. In the example of the hammer and nail, it seems the hammer exerts a force and the nail receives it—or is it the other way around? Newton believed that it didn’t matter. It was his opinion that nature is balanced and both objects are equal in terms of force. In the case of the hammer and nail, Newton would have said, "The same force that drives the nail also decelerates the hammer." This is the basis for his third law: Whenever one body exerts a force against another, an equal and opposite force exists between the bodies. This is often stated as, "For every action, there is an equal and opposite reaction."
Newton firmly believed this reaction between bodies had a great deal to do with motion. For example, if you lean against a wall with a force, the wall reacts with an equal force. It may be difficult to believe a lifeless object such as a wall exerts a force, but consider our example carefully. Place a piece of paper between you and the wall. The force of your leaning against the wall is not causing the paper to accelerate. Therefore, the wall must be exerting an equal amount of force against the paper.
007. Circular motion and the forces involved
Up to this point, we have discussed motion in a straight line. Recall that Newton’s first law of motion states that a body will remain in a constant state of motion if no force interferes with that motion. Therefore, in order for objects to move in other than a straight line, other forces must act upon the body. The forces discussed here will be of great importance in understanding the motions in the atmosphere we discuss later.
Centripetal force
Most physics textbooks define centripetal force as a center-seeking force causing objects to move in a circular path. This might lead you to believe that, to get an object to move in other than a straight line, you need a centripetal generator or some such contraption. There is no such thing as a centripetal generator, but objects in space move in circular orbits for a specific reason. From our discussion on gravity, remember the force of gravity is an attracting force that affects every object in the universe. It is the "pull" of gravity that causes smaller bodies in space to orbit larger ones. Imagine a comet moving through space in a straight line. If the comet comes close to a body with enough mass (such as the star in figure 1–6), it will be attracted to the larger mass and it will begin to move in a somewhat circular path around the star. The force responsible for attracting the comet is not centripetal—it is gravity.
Now take for example a ball on a string; if you hold the string and begin swinging the ball, it will move in a circular path around your hand. The force causing the ball to move in a circle is the result of you holding the string, not of centripetal force.
Any object moving in a circular path has an external force acting on it that is perpendicular to the object’s path and pointed toward the axis of circulation. This force may be gravity, you holding a string tied to a ball, or between a planet and its moon. In conclusion, centripetal force is any force that deflects an object from a straight path.
Centrifugal force
Newton said that for every action there is an equal and opposite reaction. If this is true, then for objects moving in a circular path, there must be some force acting against the center-seeking force. This reaction is termed centrifugal force. Where does it come from? Think about the ball on the string; there is no force pulling the ball outward. The only force acting on the ball is the inward pull of the string. The opposite reaction to that force is the outward pull of the ball against the string. If the string breaks, the ball will not move outward on a curved path—it will move in a straight line perpendicular to the line created by the string at the moment it breaks (fig. 1–7). Centrifugal force is inertia resisting the inward force of the string.
Now let’s look at centrifugal force from another frame of reference. Imagine that the ball on the string is hollow and is partially filled with water. If the ball is not accelerating, the water will rest in the bottom of the ball. If the ball is twirled on a string, what happens to the water? It is forced to the side of the ball away from the string or opposite to the center-seeking force shown in figure 1–8. The force responsible for this is centrifugal force.
The strength of centrifugal force is dependent on three things—mass, velocity, and radius of rotation. Centrifugal force is directly proportional to mass and velocity, and inversely proportional to radius of rotation. This force is illustrated every time you exit off the interstate. As you turn the wheel of your vehicle, you begin to feel an outward-pulling force. To compensate for this outward pull, you apply the brakes, thus decreasing your velocity. Now imagine two vehicles traveling at the same speed and entering the exit ramp. One vehicle is a small sports car and the other a tractor trailer. The tractor trailer will experience a much greater centrifugal force because of its larger mass.
If an orbiting object is accelerated, centrifugal force will become stronger than the balancing center-seeking force. For example, if you swing a heavy ball fast enough, it will break the string. The same is true when gravity is the center-seeking force. This idea was used to get spacecraft out of the Earth’s gravitational field to fly to the Moon.
Coriolis force
Coriolis force is a force created by the rotation of the Earth that acts on any body moving above the Earth’s surface. This force causes objects in motion to be deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. Because coriolis is a force, you would expect that it causes an acceleration on a moving object. Actually, the deflection due to coriolis is an illusion, or often referred to as an apparent force.
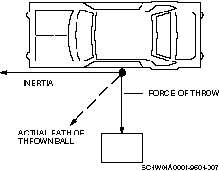
To help you understand what the coriolis force really is, let’s consider a parallel event. Imagine throwing a rubber ball at a car that is moving from right to left past the point where you are standing. If you throw the ball straight at the car the exact instant it passes you, the ball will miss its target to the right. To hit the car, you must throw the ball at some point ahead of the car before the car passes directly in front of you. Now imagine being in the car trying to hit a stationary object with the ball as you pass the object. If you don’t throw the ball at some point before you are directly in front of the object, it will again miss its target to the right. Figure 1–9 illustrates the reason. There are actually two forces acting on the ball as it leaves your hand: the force you use throwing the ball and the inertia from the forward motion of the car. The path the ball travels is the vector sum of the two forces following Newton’s second law.
Now consider two points on the Earth, both on the same line of longitude: one at the North Pole, the other at the Equator. Both points make exactly one revolution per day around the pole. Still, as a stationary observer in space, you would see that the point at the Equator is moving faster than the point at the pole. Because the Earth’s circumference is greater at the Equator than at the pole, the point at the Equator is moving faster. This is similar to two people running around a circular track, one on the inside and the other on the outside. The runner on the outside must run faster to complete a lap in the same time as the runner on the inside—the runner on the outside of the track has farther to run.
Again, from your stationary platform in space, imagine that a missile is launched from the North Pole toward a target on the Equator as seen in figure 1–10. As you observe the missile, it flies in a straight line; but, when it reaches the Equator, its target has moved out of the way because the target is moving faster than the point of launch. To the person who launched the missile, it would appear as if the missile had veered to the right of its target. This is the same effect you got when you tried to hit the moving car with the ball.
Figure 1–10. Coriolis affecting a southward moving projectile.
If we reverse the missile and target positions as in figure 1–11, the same thing will happen except this time the target is moving slower than the launch point. This would be the same as when you throw a ball from a moving car at a stationary object. The missile, like the ball, has two forces acting on it, and its path will be the vector sum of those two forces.
Figure 1–11. Coriolis affecting a northward moving projectile.
Self–Test Questions
After you complete these questions, you may check your answers at the end of the unit.
004. The quantities of motion and computing their elements
1. Match the elements of motion in column B with the proper definition in column A. Some column B items may be used more than once.
Column A |
Column B |
____1. This element is measured in dynes. ____2. This element is expressed as distance per unit time. ____3. This element has magnitude and direction. ____4. This element may be a change in direction or speed. ____5. This element is mass times acceleration. ____6. This element is a change in rate. |
a. Speed or rate. b. Velocity. c. Acceleration. d. Force. |
2. An aircraft climbed from 10,000 feet to 25,000 feet in 3 minutes. What was its rate of climb per second?
3. During the same climb, the aircraft’s speed decreased from 450 to 300 knots. What was the aircraft’s acceleration per minute?
4. During the last observation, the winds were reported as 210° at 15 knots. What is the wind velocity?
5. How much force, in dynes, will it take to accelerate a mass of 4 kilograms at 20 meters per sec2?
005. The force of gravity
1. Given two objects, each of a different mass separated by a distance, what will happen to the gravitational force if:
a. The mass of object 1 is reduced?
b. The mass of object 2 is increased?
c. The objects are moved closer together?
2. Given an object with a mass of 200 grams and a value for acceleration due to gravity of 980 cm per second per second ![]() compute the force exerted by the object.
compute the force exerted by the object.
006. Laws of motion
In each of the following situations, state which of Newton’s laws is demonstrated:
1. Your car stalled in an intersection, and you must push it out of the way. No matter how much you strain, you can’t get the car rolling until someone helps you. Once the car is rolling, you find you can keep it going with little effort.
2. A football kicked into the wind flies 50 yards before if first touches ground. The same football kicked with the same force in the opposite direction flies 60 yards before first touching ground.
3. A pistol recoils when fired.
007. Circular motion and the forces involved
1. Which force is any force that causes a body to veer from a straight path?
2. If a bucket of water is swung perpendicular to the ground, what force keeps water in the bucket from falling out, even when the bucket is upside down?
3. In circular motion, what force acts against the inertia of the moving object?
4. What force causes objects to veer from their intended path on a rotating platform?
5. What force is the equal and opposite reaction to center-seeking forces?
6. What force appears to cause objects in the southern hemisphere to be deflected to the left of their intended path?
Thus far, we have discussed some very basic elements of physics. Now that you understand those basic elements, we can begin to discuss the physical elements that are more directly related to the study of our atmosphere. In this section, we discuss the atmospheric quantities of pressure, density, and moisture.
008. Measures of atmospheric substance
In this lesson we discuss pressure and density and the different ways that we measure each.
Pressure
As a quantity in physics, pressure is the ratio of force to area. The formula for computing pressure is as follows:
P = ![]()
where:
P = Pressure.
F = Force.
A = Area.
To understand completely the computation of pressure, let’s first examine its individual elements.
Force, as you have learned, equals mass times acceleration. Therefore, we can use acceleration due to gravity (approximately ![]() ) to compute the force between every object on Earth and the Earth itself. Remember that this force is toward the center of the Earth. Therefore, if an object has a mass of 10,000 grams, it exerts a downward force equal to 9,800,000 dynes (10,000 grams ×
) to compute the force between every object on Earth and the Earth itself. Remember that this force is toward the center of the Earth. Therefore, if an object has a mass of 10,000 grams, it exerts a downward force equal to 9,800,000 dynes (10,000 grams × ![]() ). If you place your hand between this object and a table, you can feel this force. This is commonly called weight—in our 10,000 gram object, about 22 lbs.
). If you place your hand between this object and a table, you can feel this force. This is commonly called weight—in our 10,000 gram object, about 22 lbs.
Suppose the object is in the shape of a brick, with the area of one side measuring 100 cm2 and the other 10 cm2—this is where area comes into the picture. The brick weighs 22 lbs regardless of which end it is resting on. Why would it be more comfortable to have the larger end resting in your hand? Because there is more pressure being exerted under the smaller end than under the larger end of the brick. To show the difference in pressure under each side, use the formula to compute the pressure under each side of the brick. We show this below, substituting weight for force in the formula:
Small side:
P = ![]() =
= ![]()
Large side:
P = ![]() =
= ![]()
With the larger side resting on your hand, each square centimeter of your hand under the brick is supporting only 0.22 pounds; under the small side of the brick, each square centimeter of your hand is supporting 2.2 pounds. Each of these is a measure of the pressure exerted on your hand by the brick.
Pounds per cm2 is a measure of pressure, but not one with which you are familiar in meteorology. The pressure measurements you use on a day-to-day basis are expressed in millibars (mb) or inches of mercury.
Millibars
The bar is the basic unit of pressure in the MKS system of measurements. From our study of prefixes used in measurements, you have probably concluded that a millibar is one-thousandth of a bar. Because the millibar is a more exact unit of measure, it has become the basic unit of measure for atmospheric pressure in the international system. The millibar is equal to the force of 1,000 dynes per square centimeter. To convert dynes per cm2 to millibars, divide the force in dynes 1,000; therefore, 6,500 dynes divided by cm2 equals:
![]() = 6.5mb
= 6.5mb
Inches of mercury
This measure of pressure is simply the height that a vertical column of mercury is displaced upward by the weight of the atmosphere measurements. Inches of mercury is the standard measure of atmospheric pressure used in the FPS system of measurements. A pressure measurement of 1 inch of mercury is equal to 33.865mb.
Density
Density is the property of matter that allows us to distinguish between various types of matter and is represented by the Greek symbol Rho (r ). Density is why some objects of the same size have different weights. This characteristic of matter is the measure of mass per unit volume and is represented by the formula:
r = M/V
where:
r = Density.
M = Mass.
V = Volume.
For example, if an object has a mass of 60 grams and a size of 10 cm3, the object’s density is as follows:
r
= ![]()
r
= ![]()
To compare this to an object with a mass of 75 grams occupying 15 cm3, again compute the mass per unit volume:
r
= ![]()
r
= ![]()
With the density properly computed as shown above, you can readily see that the first object is denser and weighs more under the same conditions of temperature and pressure.
Because the volume of matter varies with temperature and pressure, density also varies with temperature and pressure. For example, you know that 1 cm3 of water at 4°C has a mass of 1 gram. According to the density formula, this gram of water has a density of ![]() . Yet the density of a gram of water at 20°C is given as
. Yet the density of a gram of water at 20°C is given as ![]() . The reason for this is that water, like all matter, expands when it is heated. Expansion of matter equates to an increase in the volume that the matter occupies. Using what you learned about variation, you can see that if volume increases in the formula, then density must decrease.
. The reason for this is that water, like all matter, expands when it is heated. Expansion of matter equates to an increase in the volume that the matter occupies. Using what you learned about variation, you can see that if volume increases in the formula, then density must decrease.
Water’s change in density due to change in temperature is very small (0.2 percent). This is the case with most matter, especially liquids and solids. However, the density of gaseous matter (such as the atmosphere) is totally different. Imagine two, cylinders, each with an inserted plunger, one filled with water and the other with air. If you pushed down on both plungers with an equal amount of force, the pressure in each cylinder would increase equally. Yet the volume in the container of air would decrease while the volume in the container of water would remain the same. Since the volume in the container of air decreases, the density increases. The volume in the container of water remains the same; therefore, its density remains the same.
From this experiment, you can see that it is very important that you compare the density of matter under identical conditions or, at least, that you have the conditions of the measurement expressed. You have also seen that the density of gas is affected more by changes in pressure and temperature than is water. Changes in temperature also have a similar effect on the density of gas. We discuss these and other peculiarities of gasses later.
009. Measures of moisture in the atmosphere
Moisture in our atmosphere is one of the most important elements in the study of meteorology. Obviously, without it there would be no clouds or rain; beyond that, the amount of moisture in the atmosphere has a great effect on how the atmosphere behaves. For example, as water vapor content increases, the air becomes less dense and rises—a sign of an unstable atmosphere. As you know, an unstable atmosphere is conducive to thunderstorm development.
Water vapor pressure
Water vapor pressure is a measure of the amount of water vapor in the atmosphere. From the last lesson you know that atmospheric pressure is the weight of a column of air over a given location. Since water vapor is a gas, it is included in the measure of atmospheric pressure. The English physicist Dalton proved that the pressure of a fixed volume of gas was equal to the sum of the partial pressures exerted by each different gas within the volume. The amount of water vapor pressure in a column of air depends greatly on the temperature of the column of air. Thus, as you may recall from earlier schools, warm air can hold more water vapor than cold air.
Vapor pressure
Vapor pressure (not to be confused with water vapor pressure) is a measure of the ability of a moisture source to exchange water molecules with the surrounding air. For example, the vapor pressure of a body of water or ice refers to the vapor pressure in the minute space immediately above the surface of the body of water or ice. Comparing the two, we find that vapor pressure is greater over water than over ice. The reason for this is that the molecules of water, warmer than those of ice, move about more freely. This increased molecular activity allows the molecules of water to escape or evaporate into the atmosphere more readily.
Saturation vapor pressure
Water molecules are constantly in motion, constantly changing the water’s state from liquid to gas; solid to gas; liquid to solid, etc. When the number of molecules escaping and the number returning are equal, saturation vapor pressure is reached. Since saturation vapor pressure is temperature dependent, it varies directly with temperature.
Relative humidity (RH)
Relative humidity is the ratio of actual water vapor in the air to the amount it can hold. You learned in the basic weather course how to compute this by using a psychometric calculator. You can also determine relative humidity from the ratio of vapor pressure to saturation vapor pressure:
RH % = ![]() (100)
(100)
where:
RH = Relative humidity.
e = Vapor pressure.
es = Saturation vapor pressure.
100 = Value used to convert decimal to percent.
Therefore, if the vapor pressure (e) equals 35mb and the saturation vapor pressure (es) equals 80mb, compute relative humidity as follows:
RH % = ![]() (100)
(100)
RH % = ![]() 100
100
RH % = 0.4375(100)
RH = 43.75%
Relative humidity is the most commonly used expression of water vapor content in the atmosphere.
Mixing ratio
Because saturation vapor pressure and relative humidity vary with temperature, they are not exact measures of water vapor content. Therefore, we often use another measure—mixing ratio. Mixing ratio is the mass of water vapor (Mv) compared to the mass of dry air (Md) contained in a volume of natural air.
NOTE: Dry air is air with all the moisture removed. Natural air is dry air plus water vapor.
Mixing ratio is a more accurate measure of water vapor because of the nature of mass. Remember that the only way to change mass is to add or remove matter. The mixing ratio is expressed in grams per kilogram (g/kg), and the formula for computing it is as follows:
w = ![]()
where:
w = Mixing ratio.
Mv = Mass of water vapor.
Md = Mass of dry air.
Although we can use this formula to compute mixing ratio, the simplest way to compute this value would be by using a plotted Skew-T, Log P diagram. The procedure for finding the mixing ratio for a given pressure is accomplished by reading the value directly (or by interpolation) of the saturation mixing-ratio line that crosses the dew-point curve (Td) at that pressure. For example, if the 700-mb Td is –13° C; the intersection of the saturation mixing-ratio line and the –13° C Td isotherm at 700mb would equate to a mixing ratio of:
![]()
Absolute humidity
Absolute humidity is another expression of mixing ratio. We express it as a percent; therefore, to compute absolute humidity, we multiply mixing ratio by 100.
Specific humidity
Specific humidity is another measure of water vapor content that uses comparison of masses—it is the ratio of water vapor to the total mass of the natural air. We also express specific humidity in terms of grams per kilogram; but, because specific humidity is the ratio of water vapor to total mass, it is always a lower value than mixing ratio or absolute humidity. The formula for specific humidity is as follows:
q = ![]()
where:
q = specific humidity.
0.622 = specific humidity constant.
e = vapor pressure.
P = atmospheric pressure.
0.378 = specific humidity constant.
Below is an example of a specific humidity computation using an atmospheric pressure of 988mb and a vapor pressure of 35mb.
Formula:
q = 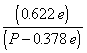
Input factors:
q = ![]()
Calculate:
q = ![]()
q = ![]()
Answer:
q = 0.022 grams per kilogram
NOTE: Specific humidity calculation is preferable for very precise physical and theoretical work. For synoptic purposes, however, the mixing ratio is sufficiently representative and is easier to evaluate.
Self–Test Questions
After you complete these questions, you may check your answers at the end of the unit.
008. Measures of atmospheric substance
Determine if the following statements pertain to pressure or density:
1. Is equal to ![]() .
.
2. Is equal to ![]() .
.
3. Increases in temperature cause it to decrease.
4. A single object may have variations of this quantity from one side to the other.
5. Decreasing the space that matter occupies causes this quantity to increase.
6. The millibar is an example of this quantity used in meteorology.
009. Measures of moisture in the atmosphere
1. Match the measures of humidity in column B with the definitions in column A. Column B items may be used more than once.
Column A |
Column B |
____1. Indicates an equal exchange of water vapor between the air and a moisture source. ____2. Affected by temperature. ____3. Ratio of actual water vapor to amount of water vapor that a quantity of air can hold. ____4. Partial pressure of the atmosphere due to the presence of moisture. ____5. Ratio of mass of water vapor to mass of dry air. ____6. These two measures of atmospheric moisture are the same. ____7. Ratio of mass of water vapor to mass of natural air. |
a. Water vapor pressure. b. Vapor pressure. c. Saturation vapor pressure. d. Relative humidity. e. Mixing ratio. f. Absolute humidity. g. Specific humidity. |
When we discussed density earlier, we compared the effect of pressure on equal volumes of water and air. You saw that, under pressure, the volume of a quantity of air could be reduced but the volume of water could not. The molecules of gas are free to move about and collide with one another. On the other hand, the molecules of liquids are cohesive—they tend to stick to one another. This is why the volume of water could not be reduced while the volume of air could.
In this section, we further explore the behavior of gases through discussions of the gas laws. We also explore heat energy, changes in heat, and the effects of changes of state on the atmosphere.
In any gas, there is a close relationship between the variables of temperature, pressure, and volume. A change in any of the variables causes a change in one or both of the others. Understanding these relationships helps you understand the nature of the atmosphere and the weather.
Charles’ law
The two parts of Charles’ law explains the relationships between temperature and pressure and between temperature and volume. Notice that the key variable in Charles’ law is temperature in both parts.
The first part of Charles’ law states that, if pressure remains the same (constant), volume varies directly with temperature. That is, if the temperature of a quantity of air increases, its volume also increases. Imagine that a plastic bag is filled with air at room temperature, then sealed and placed in a freezer for several minutes. When the bag is removed from the freezer, it will be somewhat deflated; if the bag is allowed to warm up to room temperature, it will return to its original state of inflation.
For an easy way to help you remember these relationships, set the variables up in a proportion so that when pressure is constant:
![]() =
= ![]()
The subscript "1" represents the original temperature and volume and the subscript "2" represents the changed temperature and volume. When working with proportions, remember that, if the numerator is increased by any factor, the denominator also must be increased by the same factor. To show how it works, assume that the temperature of 6 cm3 of a gas is increased from 250°K to 300°K and pressure remains unchanged. To compute the new volume, substitute the variables and solve as follows:
![]() =
= ![]()
250 (V2) = 300(6)
250 (V2) = 1,800
V2 = ![]()
V2 = 7.2 cm3
As you can see, volume did definitely increase with temperature. Notice that it was not necessary to carry units of measure through the entire process. Just be sure that you express all measures of volume and temperature in the same respective units.
The second part of Charles’ law states that, with volume constant, pressure varies directly with temperature. We can illustrate this by using a jar with a lid that seals. Allow the jar to become warm by placing it on or near a heat source. When the jar is warm, place the lid on it and place it in the refrigerator. After a time, remove the jar and remove the lid. As the seal breaks, you will hear a hiss because the pressure in the jar decreased.
We can also use a proportion to express the relationships in this part of Charles’ law. If volume remains constant, then:
![]() =
= ![]()
Let’s use the formula to show the pressure change in our experiment above. Remembering that the jar’s volume is constant, assume you heated it to 50°C and the pressure was 1,000mb. If the jar cooled to 5°C in the refrigerator, you could substitute the values and solve as follows: (You must convert all temperatures to degree Kelvin to use this formula).
![]() =
= ![]()
![]()
323(P2) = 1,000(278)
323(P2) = 278,000
![]()
P2 = 861mb
Notice again that temperature is the numerator in the fractions. The reason for this is that temperature is never held constant in either part of Charles’ law. Therefore, if volume is the constant, then pressure is the denominator; if pressure is the constant, then volume is the denominator. This will make it easy for you to remember the two parts of Charles’ law.
Boyle’s law
Unlike Charles’ law, Boyle’s law uses temperature as a constant to explain the relationships between pressure and volume. Therefore, pressure and volume vary inversely. An example would be a bicycle tire pump; when you push down on the handle, the volume in the cylinder of the pump is reduced. This results in an increase in pressure at the nozzle.
We can illustrate the reverse of this by using a weather balloon filled with helium. Since pressure decreases with height, even if the temperature of the helium is held constant, the balloon expands. Therefore, volume is inversely proportional to pressure.
Since Boyle’s law always uses temperature as a constant, only one proportion is needed to express the law:
![]()
Notice that original volume and pressure are the extremes of the proportion, while the new volume and pressure are the means. To show that this proportion works, let’s assign values to the example of the weather balloon. Assume that the pressure at the surface is 1,000mb at release and the volume of the balloon is 2 cubic meters (m3 ). We now use the formula to show what happens if the balloon rises to a level where the pressure is 500mb:
V1 = 2
V2 = x
P2 = 500
P1 = 1,000
Therefore:
![]()
![]()
![]()
x = 4
As you can see, the pressure decreased by 1/2 while the volume increased by the reciprocal, or 2.
Equation of state
The equation of state is a general gas law used for finding pressure, temperature, or density of a dry gas by using a gas constant. In Charles’ law, either pressure or volume was held constant; in Boyle’s law, temperature was held constant. Therefore, if we allow temperature, pressure, and volume to vary, as they do in the atmosphere, we have to use a combination of laws. Also, gases in the atmosphere are not confined to a container. Therefore, we use the relationship between mass and volume (density) in the formula rather than volume.
We can best explain the relationship between the variables in the equation of state by looking at the formula:
P = r × R × T
where:
P = Pressure in millibars.
r = The density.
R = The specific gas constant (2.87 when r is expressed in Kg/cm3).
T = The temperature in degrees Kelvin.
Now let’s examine the relationships as we hold different variables constant. If pressure is constant, temperature and density vary inversely; for example, as temperature increases, density decreases and vice versa. With density held constant, pressure and temperature vary directly; that is, with no change in mass, if pressure increases, so does temperature. If temperature is held constant, then density and pressure vary directly; for example, if there is no change in temperature and pressure increases, so does density.
We can use the relationship between the three variables to explain why cold Canadian air has high pressure. For example, as the temperature falls, pressure increases. This seems to go against the relationship between pressure and temperature; nevertheless, as the pressure increases, with the decreasing temperature, density also increases to satisfy the gas law. To show it mathematically, assume an air mass has a pressure of 1,000mb, a density of 1 Kg/cm3, and a temperature of 280°K. If the temperature drops to 263°K and the pressure increases to 1,020mb, density changes as shown here:
P = r × 2.87 × T
1,020 = r × 2.87 × 263
1,020 = 754.81(r )
r = 1,020/754.81
r
= ![]()
As you can see, density increases to ![]() to satisfy the equation.
to satisfy the equation.
011. How atmospheric gases change temperature
As you have seen, the measure of heat or temperature greatly influences the behavior of gasses. For example, variations in temperature cause changes in the pressure and volume of a gas. No less important is the effect temperature has on the way air behaves in our atmosphere. From the resident courses, you know that, as air is heated, it rises—it becomes less dense than surrounding air. You also realize that, if air is cooled, it sinks. Therefore, it is important to understand how heat is added and removed from air.
There are two processes by which the temperature of gasses are changed. The first is by the introduction of heat from an outside source, or diabatic heating. The other method involves no transfer of heat from an outside source, or adiabatic heating.
Diabatic processes
As we mentioned above, this method of heating a volume of air involves the introduction of heat or thermal energy from an outside source. There are three diabatic processes for changing the temperature of a parcel of air:
Conduction
Conduction is the process of transferring thermal energy through direct contact. When you place a pan of water on the heating element of an electric stove, the bottom of the pan is heated by conduction. The water in contact with the inside of the pan is also heated by conduction. Gas or air is also heated through contact with a warmer surface. For example, as an air mass moves over land or water that is warmer than the air, the air mass is heated from below via conduction.
Air also can lose heat through the process of conduction. If a warm body of air contacts a cooler surface, thermal energy from the air is transferred to the cooler surface.
Radiation
This is the process of individual air molecules absorbing radiated energy as heat. For example, a portable electric heater heats surrounding air through the radiation process. In the atmosphere, radiation from the Sun is absorbed by the Earth and then reradiated back into space as infrared radiation. During the reradiation process, some thermal energy (infrared radiation) is absorbed by air molecules, causing a rise in temperature.
Air, like any mass, radiates energy; therefore, a gas cools through the radiation process. This is true no matter how the air is heated.
Convection
This is the process by which most heat is transferred in a volume of air. In each case above, when the air was heated, it rose and was replaced by cooler air. This sets up a motion known as a convective current that causes a mixing or exchange of mass between colder and warmer bodies of air. Ultimately, individual molecules receive or lose heat through contact or radiation; still, these processes are enhanced by the added mixing of convective currents.
Adiabatic process
In each diabatic process, you saw that heat was added by an external source in one form or another. In the adiabatic process, volumes of gases change their temperature without the introduction of heat from an outside source or loss of heat to an outside source.
Adiabatic heating
From Charles’ law, remember that, when volume is held constant, temperature varies directly with pressure. In other words, an increase of pressure in a fixed volume causes an increase in temperature. As pressure is added to a car tire, the tire becomes warmer. This is the basis for the adiabatic process of heating a parcel of air in the atmosphere. Since pressure in the atmosphere increases as you near the surface, a descending parcel of air undergoes an increase in pressure and warmth. For example, the warm Chinook winds on the leeside of the Rocky Mountains are heated adiabatically as they descend the mountain slopes.
Adiabatic cooling
Adiabatic cooling is the reverse of the heating process. Any air parcel that rises in height experiences a reduction of pressure and, therefore, an expansion of volume and cools—also by Charles’ law. This is why the air cools and clouds form on the windward side of the Rockies—the air is cooled as it moves up the mountain slopes.
Adiabatic lapse rate
A lapse rate is the rate at which temperature changes with a corresponding change in pressure or height. This rate is said to be adiabatic if it equals the rate expected due to adiabatic heating or cooling. In meteorology, the adiabatic rate is expressed in terms of change in temperature per increment of height. Remember that a change in height means a change in pressure. There are two adiabatic lapse rates—dry and moist.
The dry adiabatic lapse rate is used for air that contains moisture but has a relative humidity of less than 100 percent. This rate is equal to 10°C per kilometer (3°C per 1,000 feet) of upward or downward motion. At this rate, air at a temperature of 25° C (77°F) rising to a height of 20,000 feet (6 km) is cooled to –35° C (–31°F). The rate for moist air (saturated, or 100 percent RH) varies with temperature and pressure, but is approximately 6°C per kilometer (2°C per 1,000 feet).
To understand the various changes of state, you must understand the difference between temperature and heat. Heat is a quantity that you can feel as radiated or conducted energy. As you know, heat can be transferred from one body to another through the processes of radiation, conduction, convection, and advection.
Temperature
Temperature is a measure of heat or, as we said earlier, a measure of thermal energy. The higher the measure of temperature, the more thermal energy a body has.
Measures of heat energy
A calorie is a measure of thermal energy. One calorie is the amount of heat required to raise the temperature of 1 gram of water 1 Celsius degree. In the metric system, the calorie is the unit of measure for measuring heat. The British system of measurements uses the British thermal unit (BTU). One BTU is the amount of heat required to raise the temperature of 1 pound of water 1 Fahrenheit degree. Heat transferring devices, such as furnaces or air conditioners, are rated by their ability to transfer heat—this rating is generally expressed in BTUs.
Specific heat
Different types of matter have different abilities to transfer or absorb heat. For example, after you remove a TV dinner from the oven, you can touch the aluminum foil covering it within a few minutes; the food remains hot much longer. Though the foil and the food both had the same amount of heat, the aluminum lost its heat very quickly. The reason for this is that different substances have different specific heats.
The specific heat of a substance is the amount of heat that is required to raise the temperature of 1 gram of that substance 1 Celsius degree. For example, since it takes 1 calorie of heat to raise the temperature of 1 gram of water 1 Celsius degree, the specific heat of water is 1.
The higher the value of the specific heat of a substance, the slower it gains or loses heat; the lower the specific heat, the faster heat is gained or lost. Therefore, since land heats and cools more quickly than water, the specific heat of land must be lower than that of water. Another example would be steel that has a lower specific heat and heats or cools faster than wood.
Objects lose heat, but the heat lost by an object is not really lost; rather, the heat is merely transferred to another object or mass. For example, if you place a hot chunk of steel into a container of somewhat colder water, the steel loses heat while the water gains heat. This exchange of energy continues until the water and the steel are the same temperature. If the water is then warmer than the surrounding air, heat is exchanged from the water to the air until they too are the same temperature.
It is important to remember that, by the exchange of heat between two masses, the temperature of both masses change. How much each mass changes temperature is dependent on the mass, the specific heat, and the temperature of each mass. A formula for determining the actual change in temperature for each mass is shown here:
(SH1)(M1)(D T1) = (SH2)(M2)(D T2)
where:
SH = Specific heat.
M = Mass.
D T = Change in temperature.
The subscript 1 is used for the object losing heat; subscript 2 is used for the object gaining heat.
To show how the equation works, let’s compute the final temperature of a mixture of 10 grams of water at 10°C and 20 grams of ammonia at 20°C. The specific heat of water is 1.000 and the specific heat of ammonia is 1.012. If we let x represent the final temperature of the solution, the change in temperature (D T1) for the ammonia will be (20 – x), the difference between the original temperature of the ammonia and the final temperature of the solution. The change in temperature (D T2) for the water will be (x – 10), the difference between the original temperature of the water and the final temperature of the solution. Substituting in the formula we have:
(1.012)(20)(20 – x) = (1.000)(10)(x – 10)
Continue by multiplying all the factors on each side.
404.8 – 20.24x = 10x – 100
Now, begin isolating the variable by adding 100 to both sides of the equation.
504.8 – 20.24x = 10x
Next, add 20.24x to both sides.
504.8 = 30.24x
To isolate x, divide by 30.24.
16.69 = x
When two substances of different temperatures are mixed, the final temperature is always between the two original temperatures. The warmer substance loses heat and the cooler substance gains heat. The final temperature of the solution because of the exchange of heat in our example is 16.69°C, which is between the original temperature of the ammonia (20° C) and water (10° C).
We have already stated that heat is energy in the process of being transferred from one object to another because of the temperature difference between them. But, how is this energy transfer process accomplished? In the atmosphere, heat is transferred by radiation, conduction, convection, and advection. Let’s examine each of these mechanisms individually to get an understanding of how they affect our weather. We’ll begin with the mechanism known as radiation. Some material in this unit was adapted from the book, Meteorology Today, by C. Donald Ahrens.
How radiation contributes to heat transfer
Have you ever noticed how warm and flushed your face feels as you stand in front of a huge bonfire on a bitterly cold evening, while the surrounding air remains quite cold? Somehow, energy from the fire is being transferred through the air with little effect upon the air itself. Your face, however, absorbs this energy and converts it to heat energy. Thus, you feel warm.
This energy is known as radiant energy, or radiation. It travels in the form of waves that release energy when they are absorbed by an object. These waves have magnetic and electrical properties, which is why we call them electromagnetic waves. Electromagnetic waves do not need a medium through which to travel. An example of a medium might be a telephone line or cable. Electromagnetic waves can even travel through a vacuum such as outer space. This can be proven by the fact that electromagnetic waves are emitted from the Sun, travel through space, and are felt here on Earth. These electromagnetic waves also travel very fast (approximately ![]() ). Let’s now explore some characteristics of electromagnetic waves. (NOTE: For the remainder of this reading, we may refer to electromagnetic waves with the words "waves" and "wavelength")
). Let’s now explore some characteristics of electromagnetic waves. (NOTE: For the remainder of this reading, we may refer to electromagnetic waves with the words "waves" and "wavelength")
Wave characteristics
Wave characteristics include low points or valleys (troughs) and high points or crests (ridges). By definition, wavelength is the distance between two points of corresponding phase in consecutive cycles. Figure 1–12 depicts two crests that are of corresponding phase and that are occurring in a consecutive cycle. We measure wavelengths from crest to crest or trough to trough in terms of micrometers (µm), which we symbolize with the Greek symbol lambda (l ). Now that we’ve discussed some characteristics of wavelength, let’s see how they apply to radiation and temperature.
Radiation and temperature
All things, no matter how large or small, emit some form of electromagnetic radiation in wavelengths. The temperature of an object primarily decides the object’s wavelength. The higher the temperature, the faster the associated electrons vibrate and the shorter the wavelength emission. By completing the following experiment, a person can visualize this theory more clearly.
Attach a 10-foot piece of rope to a pole. If you shake the free end of the rope rapidly (simulating high temperature and fast electron vibration), many "shorter" waves travel or propagate along the rope. Conversely, if you shake the free end of the rope slowly (simulating lower temperatures and slow electron vibration), "longer" waves appear and propagate on the rope. This experiment supports the fact that the higher the temperature of an object, the shorter is the wavelength and vice versa.
Stefan-Boltzman law
It may also be logical then that as the temperature of an object increases, more total radiation is emitted from that object each second. We can express this statement mathematically by using the Stefan-Boltzman law:
E = s T4
where:
E = the energy emitted per second per unit area.
s (sigma) = a constant (the Stefan-Boltzman constant).
T = the object’s surface temperature in degrees Kelvin.
Stefan-Boltzman law example
We can prove an example of this law in action by a comparison between the Earth and Sun. To simplify calculations we will not include the Stefan-Boltzman constant in the following example as our intention is not to be precise but to convey the intent of the equation. Therefore, our adjusted equation appears as:
E » T4
We know that the Sun is approximately twenty times warmer than the Earth (using Kelvin degrees). How much more solar radiation will the Sun emit than the Earth? Answer: The amount of radiation emitted is proportional (comparative relation in amount) to the fourth power of the temperature. In other words, if the Sun is twenty times warmer than the Earth, it will emit 204 times more radiation (E » T4). 204 = 1.6 × 105 more radiation that is emitted by the Sun. As we stated previously, all things emit radiation; we have just proven that the Sun emits a great deal more radiant energy than the Earth. Let’s again compare the two main radiating bodies that affect our weather, the Sun and Earth, but now, let’s determine their respective emitted wavelengths. With the previous discussions of radiation and wavelength characteristics, you should already have a good idea of how the respective wavelengths between the Sun and Earth differ.
Radiation of the Sun and Earth
How can we determine the wavelengths of the Sun and Earth respectively? German physicist Wilhelm Wien discovered a relationship and ultimate equation that can answer these questions. The equation, known as Wien’s law, is as follows:
l
max = ![]()
where:
l max = the wavelength (remember l symbolizes wavelength) in micrometers (µ) at which maximum radiation occurs.
T = the object’s temperature in degrees Kelvin.
Constant = 2897 micrometers Kelvin.
Let’s now examine an example of this equation that compares the wavelengths of the Sun and Earth. For simplification, we round the constant in the equation up to 3000 µm Kelvin (K).
Wien’s law example
The Sun’s temperature is approximately 6000°K. Let’s set up the equation to determine the wavelength at which the Sun’s maximum radiation occurs.
l
max = ![]()
Now, determine what the Earth’s wavelength at which maximum radiation emission occurs if the Earth’s surface temperature is 300°K (8 °F)? Again, let’s set up the equation:
l
max = ![]()
Wien’s law states that the wavelength at which the maximum amount of energy is emitted by an object is inversely (directly opposite) proportional to the temperature of the object. We just proved that statement in our examples. Simply put, where the temperature of the object was high (Sun), the wavelength was shorter (0.5 µm). Also, where the temperature of the object was cooler (Earth), the wavelength was longer (10.0 µm).
Long-wave/short-wave radiation
Because the Earth emits longer wavelengths, its emission is called long-wave radiation. It is also referred to as terrestrial radiation, meaning, "from the Earth." Conversely, the Sun’s shorter wavelength emission is often called short-wave radiation. Radiation from the Sun is also referred to as solar radiation, meaning, "from the Sun." We know that the Sun radiates at a maximum rate at one wavelength; however, it also emits some radiation at almost all other wavelengths. If we look at the emission of radiation at each wavelength, we can obtain the Sun’s electromagnetic spectrum or electromagnetic wavelength range. Let’s briefly discuss the Sun’s electromagnetic spectrum.
Electromagnetic spectrum
The three areas of the Sun’s electromagnetic spectrum that we discuss are the visible, ultraviolet, and infrared regions. The visible spectrum is obviously the spectrum visible to the naked eye and is comprised of the colors violet to red. The range of this spectrum is between 0.4 and 0.74 µm. (See figure 1–13.) Violet corresponds to the shortest of these wavelengths (0.4 µm) with red corresponding to the longer of these wavelengths (0.7 µm). The Sun emits nearly 44 percent of its radiation in the visible spectrum.
Figure 1–13. Electromagnetic spectrum.
Wavelengths that are shorter than the visible spectrum (< 0.4 µm) are known as ultraviolet (fig. 1–13). X-rays and gamma rays fall into this category. Seven percent of the Sun’s total energy is emitted at the ultraviolet region.
Wavelengths that are longer than 0.7 µm are called infrared. We use sensors, like those on weather satellites, to detect these wavelengths as the infrared spectrum cannot be seen by humans. Since clouds always radiate infrared energy, we can process satellite imagery using infrared sensors during both day and night. This nighttime coverage is an invaluable tool for the forecaster, especially during nocturnal severe weather events. Roughly 37 percent of the Sun’s energy is radiated in the near-infrared 0.7 to 1.5 µm range. Conversely, the relatively cool Earth emits almost all of its energy as far-infrared, 4 to 25 µm. This is understandable since infrared wavelengths are longer, which would be associated with cooler temperatures. Remember, part of Wien’s law states: Where the temperature of an object is cooler, the wavelength is longer. Now, let’s look at some other factors associated with radiation that help explain some of Earth’s atmospheric and weather peculiarities. These factors include: absorption, emission, and albedo.
Absorption, emission, and albedo
All objects not only radiate energy, they absorb it as well. Absorption is the process by which incident radiant energy is retained by a substance. This explains why the Earth doesn’t get progressively colder through the emission of long-wave radiation because it is absorbing radiation simultaneously. If the Earth radiates more energy than it absorbs, it gets colder. An example of this is a clear night. If the Earth absorbs more energy than it emits, it gets warmer. An example of this is a clear sunny day. When an object emits and absorbs at the same rate, its temperature remains constant.
Black body
Temperature, moisture, texture, and color are surface characteristics that strongly affect the rate of absorption and radiation. Let’s discuss the color characteristic and how it affects absorption and radiation. Have you ever walked barefoot on a black asphalt road on a hot sunny day? The asphalt obviously gets very hot, hotter than surrounding surfaces such as dirt and grass. This is because the black asphalt is a good absorber of short-wave radiation. The asphalt converts energy from the Sun into internal energy, usually increasing its temperature.
Good absorbers are also good emitters of radiation. Let’s go back to the asphalt example. Once the Sun sets, the asphalt cools quickly and is usually cooler than the surrounding dirt and grass by the time morning arrives. Objects that are perfect absorbers (absorb all the radiation that strikes them) and perfect emitters (emits all possible radiation) are called black bodies and are considered ideal objects. The Earth and Sun are assumed to be black bodies.
Radiative equilibrium temperature
If we say that the Earth and Sun are black bodies and therefore absorb and emit radiation equally, a state of radiative equilibrium is achieved. The average at which this occurs is called the radiative equilibrium temperature. Because of the Earth’s distance from the Sun (93 million miles), its radiative equilibrium temperature is about –4°F! This is much lower than the observed average temperature on Earth of 59°F. What could cause this difference?
One factor that we haven’t discussed yet is the Earth’s atmosphere and its ability to absorb and emit radiation. Unlike the Earth and Sun, the atmosphere does not behave like a black body. It is considered a selective absorber because it selectively absorbs and emits radiation. In other words, it is a good absorber at certain wavelengths but may not be a good absorber of all wavelengths. There is a law in physics that speaks specifically about this phenomenon. Let’s discuss it now.
Kirchoff’s law
Kirchoff’s law says that good absorbers of a certain wavelength are good emitters at that wavelength. Some gases in the atmosphere are selective absorbers. The ozone is a good example of this. We’ve all heard of ozone depletion due to added chlorofluorocarbons (CFCs) in the atmosphere. The reason why the ozone is so important is that it protects the Earth from harmful ultraviolet radiation because it selectively absorbs this wavelength.
Carbon dioxide (CO2) and water vapor are also both selective absorbers and emitters. These gases are abundant in the lower atmosphere of the Earth. As the Earth radiates its energy at far-infrared wavelengths, CO2 and water vapor absorb a large portion of this radiation. This absorption increases the kinetic energy (energy of motion) of these gases. These gases (CO2 and water vapor) collide with oxygen and nitrogen molecules which increase the average kinetic energy of the air. The net result of this absorption is that the lower atmosphere warms.
As CO2 and water vapor selectively absorb infrared radiation, they also selectively emit infrared radiation in all directions. Some of this energy is radiated back toward the Earth’s surface where it is absorbed and heats the ground. At this point, the process of the Earth radiating infrared wavelengths continues.
This cycle is popularly known as the greenhouse effect. The addition of cloud cover enhances this effect as the associated tiny cloud droplets are also selective absorbers of infrared wavelengths. This is why calm, cloudy nights are usually warmer than calm, clear nights whereas, calm, cloudy days are cooler than calm, sunny days. If these selective absorbers were not present in the atmosphere, Earth’s mean radiative equilibrium temperature would be closer to the –4°F stated earlier!
We have just showed that CO2 and water vapor are both good absorbers and emitters of the infrared wavelength. By doing so, we have proven Kirchoff’s law.
Conduction
The second method of heat transfer is conduction. This process involves the transfer of energy by molecular motion. During this process, the transfer of heat is always from hot to cold.
Heat conductivity
Heat conductivity, the ability of a substance to conduct heat, is related to the molecular structure (heat capacity) and density of a substance. Air is a poor conductor of heat. Soil, on the other hand, conducts heat approximately 10 times better than air while water conducts heat approximately 100 times better than air. Because air is such a poor conductor of heat, it is important as a heat transfer process only in the molecular boundary layer (i.e., the lower levels of the atmosphere). What is important about a process that only affects a small area of the atmosphere?
Atmospheric significance
We know that the surface of the Earth heats and cools by absorption and emission of solar radiation. Conduction links the surface to the air directly above it. This in turn influences low-level stability and air-mass modification. Conduction is important in transferring heat between the surface and the atmosphere but, as we stated previously, only affects the molecular boundary layer. Other mechanisms that we discuss, such as the processes of convection and advection, must act along with conduction to transport heat to and from other places of the atmosphere.
Convection
Convection is the process that vertically transports the atmospheric properties of heat and moisture. This is a much more efficient method of heat transfer than conduction. It is associated with upward vertical motions which can be initiated by any individual or combination of surface heating, low-level convergence, orographic effects, and frontal lift. The vertical extent of convection is influenced by the stability of the atmosphere. A stable atmosphere suppresses convection while an unstable atmosphere enhances convection. Convection occurs in the troposphere as the stable stratosphere acts to "cap" convection.
Advection
Advection, an important type of heat transfer mechanism, is the last of the heat transfer processes that we discuss. It involves the horizontal transport of atmospheric properties such as heat by the wind. Sometimes referred to as temperature advection, we can evaluate its strength by examining the direction and speed of the wind flow. The more closely spaced the isobars/contours, the stronger is the pressure/contour gradient and, therefore, the stronger is advection.
In the study of meteorology, there are three states in which matter may exist—solid, liquid, and gaseous. While all matter may exist in any of these states, the matter that concerns the meteorologist most is water (H2O). In the solid state, you know it as ice; in the liquid state, as water; and in the gaseous state, as water vapor. Each of these states of H2O occurs naturally in our atmosphere, which makes understanding the changing of states so important.
Changes of state
A change of state is the process of matter changing from one state to the other. Examples are water becoming ice and water becoming a gas. In meteorology, there are terms used for the various changes of state.
Vaporization
Vaporization is the change from a liquid to a gaseous state. You may know this by the more common term, evaporation. When water molecules escape to the atmosphere as water vapor, they are said to evaporate or vaporize.
Condensation
Condensation is the reverse of vaporization—the process by which water vapor becomes a liquid. Clouds and rain are the result of water vapor condensing in the atmosphere.
Freezing
This is the change of state from a liquid to a solid. You will find that water in the atmosphere does not always freeze at 0°C. Water droplets in clouds may remain in the liquid state at temperatures as cold as –20°C. For water to freeze, it is necessary that some impurities be present in the water. Condensed water in the atmosphere lacks the mineral impurities (freezing nuclei) necessary for ice crystals to form. This is also why you may need to induce freezing of the wick of the wet-bulb thermometer on the sling psychrometer—the wick is dipped in demineralized water.
Fusion
Fusion is the change from a solid to a liquid or, in other words, the melting of ice.
Sublimation
Sublimation is the change of state from a solid to a gas without an intermediate liquid stage. This is where ice changes directly into water vapor without becoming a liquid and is why snow disappears when temperatures dip below freezing.
Deposition
Deposition is the process by which water vapor changes directly into a solid. An example of this would be frost forming; water vapor in the atmosphere is "deposited" on freezing surfaces.
Exchange of heat due to changes of state
When the three states of matter change from one to another, energy (heat) is exchanged with the surrounding environment. This heat is either taken from or added to the environment surrounding the matter undergoing change.
The reason for this exchange of heat is that molecules must bond closer together or farther apart when matter changes states. For example, for liquid water to become a solid, the molecules of water must bond closer together; for water vapor to form, they must move far apart. The heat that is exchanged because of changes of state is called latent heat. Figure 1–14 shows the changes of state processes.
Changes in state that take heat
The changes in state that require a transfer of heat from the environment to the mass are the changes from a solid to a gas and all points between. These are vaporization, fusion, and sublimation.
When any of these processes occur in the atmosphere, heat is removed from the atmosphere, thus causing cooling. For example, all other factors being equal, on a hot summer day, air temperatures are several degrees cooler near a large body of water. This is due to evaporation or vaporization.
Changes in state that release heat
The changes of state that release heat to the environment are the changes from a gas to a solid and all intermediate changes. These are condensation, freezing, and deposition.
When any of these processes occur, heat is added to the atmosphere, causing a rise in the temperature. For example, when saturated air is cooled adiabatically, the moisture in the air condenses and releases heat to the atmosphere. This is why the moist adiabatic lapse rate is less than the dry adiabatic lapse rate. This is also why, if condensation occurs, such as in the formation of fog, the temperature rises slightly or does not fall as quickly.
Latent heat exchange plays a very large role in the formation of clouds and precipitation. We discuss the effects of latent heat further later in this course.
Self–Test Questions
After you complete these questions, you may check your answers at the end of the unit.
010. The gas laws
1. In Charles’ law what is the relationship between the following:
a. Temperature and pressure if volume is held constant.
b. Temperature and volume if pressure is held constant.
2. In Boyle’s law, which variable is always held constant and what is the relationship between the other two variables?
3. In the equation of state, why is density used rather than volume?
4. In the equation of state, if pressure decreases and temperature increases, what must happen to density to balance the equation?
011. How atmospheric gases change temperature
1. Match the method of heating or cooling air in column B with the definitions and descriptions in column A. Column B items may be used more than once.
Column A |
Column B |
____1. Changes due to a change in elevation. ____2. Changes due to warm air rising. ____3. Changes due to contact with a surface. ____4. Changes due to absorption of infrared energy. |
a. Diabatic. b. Adiabatic. c. Conduction. d. Radiation. e. Convection. |
012. The quantity heat
Briefly define the following terms:
1. Heat.
2. Temperature.
3. Specific heat.
4. Explain the following measures of heat energy:
a. Calorie.
b. British thermal unit (BTU).
5. Determine the final temperature of a mixture of 5 grams of ice at –10°C and 25 grams of water at 15°C. The specific heat of water is 1.000 and that of ice is 0.500.
013. Heat transfer
1. What does Wien’s law demonstrate?
2. What wavelength of the electromagnetic spectrum allows weather satellites to obtain imagery during both day and night?
3. Why do calm, cloudy nights tend to be warmer than calm, clear nights?
4. Would thick clouds or a forest have a higher albedo? Why?
5. What can be said about the Earth in terms of absorption of solar radiation and emission of infrared radiation?
6. Would soil or air have better heat conductivity? Why?
7. What is convection?
8. What can initiate convection?
9. What is advection?
014. States of matter
1. What are the three states of matter?
2. Match the changes of state in column B with the descriptions in column A. Items in column B are used only once.
Column A |
Column B |
____1. A solid becomes a liquid. ____2. A gas becomes a solid. ____3. A liquid becomes a gas. ____4. A solid becomes a gas. ____5. A liquid becomes a solid. ____6. A gas becomes a liquid. |
a. Vaporization. b. Condensation. c. Freezing. d. Fusion. e. Sublimation. f. Deposition. |
For each of the following changes of state, determine whether H2O would take heat from the atmosphere or release heat to the atmosphere.
3. Vaporization.
4. Condensation.
5. Freezing.
6. Fusion.
7. Sublimation.
8. Deposition.
On the job, the weather journeyman/craftsman attempts to forecast if the skies will be clear or if there will be clouds. This decision can ultimately affect whether an aircraft can complete its mission. Therefore, knowledge of how clouds form and dissipate is of the utmost importance to the forecaster. The science of physics plays a significant part in this process. In the previous sections, we discussed some of the aspects of atmospheric physics. In this next section we discuss physics as it applies to cloud formation and dissipation. Initially, we must understand the microphysics that ultimately lead to cloud development.
Clouds form when the atmosphere is saturated. Saturation occurs when the air holds the maximum amount of water vapor possible. At saturation, the temperature is equal to the dew-point temperature (T = Td); the vapor pressure is equal to the saturation vapor pressure (e = es); and the relative humidity is 100 percent. Saturation is a state of equilibrium. Water is constantly evaporating and condensing. The amount of water vapor molecules in the air is constant, but the actual molecules are constantly changing their state (or phase).
Cloud condensation nuclei (CCN)
The CCN are necessary for water vapor to convert to liquid. These nuclei are composed of sea salt, volcanic sulfates, forest fire smoke, clays and other fine terrestrial dust particles. These are particles on which water vapor condenses to form water droplets. The most effective nuclei are hygroscopic (water attracting) and water soluble (can be dissolved by water). If the CCN are water soluble, the resulting water droplet is not pure water but a solution. The concentration of the solution (mass of CCN to volume of water in the droplet) depends upon the size of the CCN and the amount of vapor which has condensed onto it (i.e., the volume of the droplet). Cloud droplets are initiated by the condensation of water vapor on CCN. These droplets continue to grow as water vapor condenses onto the droplet.
Initial growth of droplets
The air immediately surrounding all the droplets is said to be saturated (e = es). Initially, whether a droplet grows or not depends on saturation vapor pressure (es) of the droplet and its surrounding environment. In figure 1–15, the example on the left shows initial growth of a droplet due to the es env > es droplet and the droplet grows due to condensation. While the example on the right shows that the eenv < es droplet, therefore, the droplet shrinks through evaporation.
Figure 1–15. Comparisons between es of a droplet and its environment.
Differences in saturation vapor pressure
After their initial growth, droplets have different saturation vapor pressures based on their concentration and size. At this time, droplets grow due to solute and curvature effects. Before we discuss these effects, it is important to note that the solute and curvature effects occur between other droplets and not the environment.
Solute effect
When the solute effect occurs, droplets consisting of higher concentrations of solution have a lower saturation vapor pressure than more pure droplets (es pure > es solute). For example, let’s compare the two droplets in figure 1–16 . Droplet "b" is less pure than droplet "a", therefore esa > esb. Droplet "a" shrinks due to evaporation at the expense of droplet "b" growing due to condensation. Flow between the two factors is from higher to lower pressure.
Curvature effect
During the curvature effect, small droplets which are tightly curved have a larger saturation vapor pressure than larger droplets which are less curved (es small > es big). For example, if we have two droplets, one small and one large, the larger droplet grows at the expense of the smaller droplet. As we stated earlier, flow between the two factors is from higher to lower pressure.
Collision and coalescence
Once droplets grow large enough to fall, they can collide with other droplets and merge to form even larger droplets. Coalescence means the droplets which collide with each other stick together. This is the most efficient method of droplet growth (much more efficient than condensation). While this process is occurring the droplets still grow by condensation.
Factors that affect efficiency
Different conditions affect the efficiency of the collision-coalescence process. Now let’s discuss the factors that affect the efficiency of this process.
Residence time in the cloud
The longer a droplet remains in the cloud, the greater chance it has to interact or coalesce with other droplets. Thick clouds, such as nimbostratus, provide a greater distance for the droplet to fall, thereby increasing coalescence time. Updrafts associated with cumulus and cumulonimbus clouds account for transporting droplets to upper portions of the cloud. These updrafts also increase the distance and coalescence time of the droplet (fig. 1–17).
Figure 1–17. Factors affecting collision and coalescence efficiency.
Variable droplet fall velocities
If droplets are falling at different rates (velocities), then the faster falling droplets catch up, collide, and coalesce with the slower falling droplets. Larger droplets fall at a faster rate than smaller ones. A wide spectrum of droplet sizes is indicative of variable fall velocities.
Electric fields
Droplets exposed to an electric field develop a net charge. Opposite charges attract droplets to each other. The electrical attraction causes more collisions between droplets to occur.
Initiation and growth of ice crystals
Ice nuclei (IN), which are similar to CCN, are necessary for liquid or vapor to form ice crystals. Water droplets at temperatures below 0°C are called supercooled. These droplets exist in a liquid state. If these droplets encounter an ice crystal, they automatically freeze onto the ice crystal. Once a crystal is formed, it grows by deposition (conversion of water vapor to ice). This is because the saturation vapor pressure over ice is less than that over water (es ice < es water).
Therefore, the ice crystals grow at the expense of water droplets. Figure 1–18 shows an example of a supercooled water droplet on the left and an ice crystal on the right. Since the es over ice is less than that of a water droplet, the ice crystal grows by deposition.
Once the crystal grows large enough, it undergoes a process similar to collision-coalescence. The crystal can collide with other cloud droplets. If the cloud is colder than 0° C, the droplets freeze on contact. The crystal can also collide with other ice crystals. This process is responsible for the formation of large snowflakes.
In the previous lesson we discussed the very small-scale elements that are conducive to cloud formation. In this lesson, we discuss the larger, more general atmospheric dynamics that must also be available for clouds to form. We conclude by discussing the dynamics that lead to cloud dissipation.
Generally, cloud types and amounts are determined by the amount of atmospheric moisture available, temperature, stability, and lifting mechanisms. Let’s discuss these general cloud dynamics now.
Atmospheric moisture
First and foremost, there must be enough available atmospheric moisture present for clouds to form. No amount of lift or cooling will produce clouds if sufficient moisture is not present.
Temperature and stability
Cooling processes such as adiabatic cooling and radiational cooling are the principle condensation mechanisms. Adiabatic cooling is the most effective means of cooling water vapor until it condenses.
Lifting mechanisms
Lifting mechanisms include orographic lift, frontal lift, and low-level convergence.
Orographic lift
Horizontal motion is converted to vertical motion proportional to the slope of the terrain. Even relatively flat terrain may have slopes of 1 mile vertical to 200 miles horizontal. Craftsmen must have a thorough grasp of geographic details over the forecast region to assist in the cloud forecast. This phenomenon occurs quite often on the windward side of mountains.
Frontal lift
The amount of frontal lift depends on the frontal slope. The frontal slope is significant because it represents the potential lift of a front. A steep slope suggests the frontal lift could be strong if the wind flow forces air to ascend the frontal surface. Conversely, a shallow slope suggests the frontal lift would be weak if the wind flow forces air to ascend the frontal surface.
Low-level convergence
Convergence is a measure of the rate of the net addition of mass into a volume at a given point. This convergence can be directional, speed, or a combination of both. The mass of air converging in the low levels just above the surface must go somewhere. Since it cannot go into the ground, it rises, giving lift to the air.
Directional convergence
Directional convergence is the coming together of wind flow, which results in mass being added to an area.
Speed convergence
Speed convergence is caused by winds rapidly decreasing speed downstream. The higher speed winds push mass into an area faster than it can be removed by the slower speed winds, thus increasing the mass.
Cloud dissipation
Just as there were a number of reasons for cloud formation, cloud dissipation also has more than one reason for occurrence.
Evaporation of water droplets and the sublimation of ice crystals (conversion from ice directly to vapor) are ways that clouds can dissipate. These dissipation dynamics are caused by two mechanisms, decreasing the moisture and increasing the air temperature.
Decreasing the moisture
Decreasing the moisture of the cloud can be accomplished in two ways. The first includes the cloud "raining itself out". The precipitation evaporates while it falls or after it reaches the surface.
Moisture can also be decreased by a process known as dry-air entrainment as in figure 1–19. Dry-air entrainment is the process by which the outer edge of the cloud mixes with dry air outside of the cloud. This outer edge of cloud then evaporates or sublimates with the drier air.
Increasing the air temperature
Increasing the air temperature within the cloud can also be accomplished in two ways. The first includes adiabatic warming associated with downward vertical motions (sinking air) These motions occur with either subsidence or as a leeside mountain effect where moist air is compressed and warmed. The cloud either evaporates or sublimates.
An increase in cloud temperature can also be achieved by warming from below. For example, increased air temperature is the primary mechanism for the dissipation of radiational fog. The factor that increases the air temperature of the fog (a cloud on the ground) is solar heating.
Self-Test Questions
After you complete these questions, you may check your answers at the end of the unit.
015. Cloud microphysics
1. What two effects cause differences in saturation vapor pressure (es) in terms of CCN growth? Explain these effects assuming that the environment and air surrounding the droplet are saturated.
2. Would you expect greater collision-coalescence of a droplet to occur with stratus clouds or cumulonimbus clouds? Why?
3. A large array of droplet sizes would be indicative of what?
016. Cloud dynamics
1. A cold front has a slope of ![]() (1 mile rise over 50 mile run). A second cold front has a slope of
(1 mile rise over 50 mile run). A second cold front has a slope of ![]() . Which front has the potential to produce more clouds? (Assume each has the same stability and atmospheric moisture present.) Why?
. Which front has the potential to produce more clouds? (Assume each has the same stability and atmospheric moisture present.) Why?
2. Your station has winds of 270° at 25 knots and winds 20 miles to the east of your station are 270° at 10 knots. Based solely on the windflow, where might clouds develop and why?
3. Your station has a north/south oriented mountain range to your east. The winds at all levels are from the west. Satellite imagery shows clouds on the west side of the mountains but no clouds are apparent to the east side of the mountains. What might be a logical explanation for this situation?
Answers to Self-Test Questions
001
1. Mass.
2. Length.
3. Time.
4. Mass.
5. (1) b, i.
(2) d, j.
(3) k, m.
(4) a, l.
(5) f, n.
(6) c, g.
(7) e, h.
(8) o, p.
002
1. a. Mass; MKS.
b. Length; FPS.
c. Time; both MKS and FPS.
d. Mass; FPS.
e. Length; MKS.
2.
|
MKS unit / prefix |
Number of base units |
|
kilo / (k) |
1000 |
|
hecto / (h) |
100 |
|
deca / (da) |
10 |
|
Base unit (gram, meter, second) |
1 |
|
deci / (d) |
0.1 |
|
centi / (c) |
0.01 |
|
milli / m |
0.001 |
|
micro / (m ) |
.000001 |
003
1. The molecules in a warm body are more active than in a cold body.
2. Thermal energy is transferred from the warm body to the cold body.
3. Celsius scale where freezing is 0° and boiling is 100° ; Fahrenheit scale where freezing is 32° and boiling is 212° ; and Kelvin or absolute scale where freezing is 273° and boiling is 373° .
4. a. 7.20° C.
b. 75.2° F.
c. 303° K.
d. 305.6° F.
004
1. (1) d.
(2) a.
(3) b, c.
(4) c.
(5) d.
(6) c.
2. 83.3 fps.
3. –50 knots/min.
4. 15 knots from 210° or 15 knots toward 030° .
5. 4 kilograms = 4,000 grams, and 20 meters per sec2 = 2,000 cm/sec2. (4,000 gm) (2,000 cm/sec2) = 8,000,000 or 8 × 106 dynes.
005
1. a. Gravitational force decreases.
b. Gravitational force increases.
c. Gravitational force increases.
2. 196,000 dynes.
006
1. Newton’s first law.
2. Newton’s second law.
3. Newton’s third law.
007
1. Centripetal force.
2. Centrifugal force.
3. Centripetal force.
4. Coriolis force.
5. Centrifugal force.
6. Coriolis force.
008
1. Density.
2. Pressure.
3. Density.
4. Pressure.
5. Pressure and density.
6. Pressure.
009
1. (1) c.
(2) a, b, c, d.
(3) d.
(4) a.
(5) e, f.
(6) e, f.
(7) g.
010
1. a. Temperature and pressure vary directly.
b. Temperature and volume vary directly.
2. Temperature is always constant; pressure and volume vary inversely.
3. Because gases in the atmosphere are not confined to a container. Since volume can vary, density, which is the ratio between mass and volume, is used.
4. Density must decrease.
011
1. (1) b.
(2) a, e.
(3) a, c.
(4) a, d.
012
1. Thermal energy that you can feel.
2. Measure of thermal energy.
3. Measure of a matter’s ability to transfer or receive heat.
4. a. Amount of heat required to raise the temperature of 1 gram of matter 1° C.
b. Amount of heat required to raise the temperature of 1 pound of matter 1° F.
5. (1.000)(25)(15 – x) = (0.500)(5)[x – (–10)]
25(15 – x) = 2.5(x + 10)
375 – 25x = 2.5x + 25
350 = 27.5x
12.7° C = x
013
1. As the temperature of an object increases, the wavelength at which maximum emission occurs is shifted towards shorter values.
2. Infrared.
3. Because clouds composed of tiny water vapor droplets are excellent absorbers/emitters of infrared radiation.
4. Thick clouds because they have a higher reflective capability.
5. The Earth absorbs solar radiation only during daylight hours; however, it emits infrared radiation continuously, both day and night.
6. Soil, because it is a better conductor of heat than air due to its molecular structure and density.
7. The vertical transport of atmospheric properties (heat and moisture).
8. Any individual occurrence or combination of: 1) surface heating, 2) low-level convergence, 3) orographic effects, and 4) frontal lift.
9. The horizontal transport of atmospheric properties such as heat.
014
1. Solid, liquid, and gaseous.
2. (1) d.
(2) f.
(3) a.
(4) e.
(5) c.
(6) b.
3. Take.
4. Release.
5. Release.
6. Take.
7. Take.
8. Release.
015
1. Solute; If the droplet has a vapor pressure that is less than the environment (es env > es droplet) then the droplet will grow due to evaporation. Curvature; Small droplets which are tightly curved will have a larger saturation vapor pressure than bigger droplets which are less curved (es small > es big). In this case, if the droplet has a larger es than the environment, it will become smaller due to evaporation.
2. Cumulonimbus clouds; The residence time in cloud would be increased as updrafts in the cloud would increase distance and coalescence time of the droplet.
3. Variable droplet fall velocities.
016
1. ![]() ; Of the two, this front has the steeper slope, stronger lifting capabilities, and the adiabatic cooling process increases faster.
; Of the two, this front has the steeper slope, stronger lifting capabilities, and the adiabatic cooling process increases faster.
2. To the east of your station due to low-level speed convergence occurring there.
3. With westerly winds, orographic lift and adiabatic cooling would produce the clouds on the windward side. However, as the wind continues to flow down the leeward side of the mountains, adiabatic warming would occur and dissipate the clouds.
Do the Unit Review Exercises (URE) before going to the next unit.
Unit Review Exercises
Note to Student: Consider all choices carefully, select the best answer to each question, and circle the corresponding letter. When you have completed all unit review exercises, transfer your answers to ECI Form 34, Field Scoring Answer Sheet.
Do not return your answer sheet to ECI.
Please read the unit menu for unit 2 and continue. è