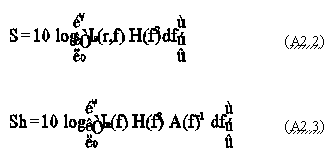
Appendix 2 E.V. Miasnikov, The Future of Russia's Strategic Nuclear Forces: Discussions and Arguments,
Previously we gave estimates of submarines detection ranges under different conditions [Miasnikov, 1993]. In this article, it was suggested that the basic detection indicators are the discrete frequencies in the low-frequency portion of the submarine's noise spectrum and that narrow-band filters are used. This approach is more effective than wide-band signal processing if sharply pronounced lines at discrete frequencies are present in the submarine's noise spectrum. As mentioned in the previous appendix, third and later generation SSNs do not have such lines at frequencies greater than 200 Hz. Moreover, it is well known that in shallow water,(28) the conditions under which we will be interested, the region of optimal frequencies for the propagation of sound lies in the 0.1-5 kHz band.
In any given region of the ocean the distance for detecting noise sources is highly variable, due to changes in both the conditions for sound propagation and magnitude of external noise. Previously we limited the estimates of the detection distance to the most favorable natural conditions, i.e., those that determine the maximum achieved magnitude. In the present work an attempt was made to take into account the variations in the natural conditions. Unfortunately, we did not have statistical information on the variability in losses by sound propagation in these conditions at our disposal, but we obtained information on the repeatability of the wind speed. Therefore, having this information allowed us to judge how frequently situations occur with which in principle, a particular detection range may be achieved.
In the current appendix, estimates of a submarine's detection distance were made for a wide band signal processing. As we showed earlier, using such an approach, one may attain slightly larger detection distances for submarines in shallow water than we previously received. However, the main conclusions which were made in the previous work, remains in force. Existing technical possibilities do not permit all enemy's SSNs to secretly carry out protracted, continuous tracking of Russian strategic submarines. This secret tracking may lead to a collision of nuclear submarines with unknown consequences.
We propose that at the entrance of the spatial filter of the receiving systems (antennas of submarine's sonar system), spectral densities of the useful signal (submarine noise which is used to detect it) and of the external noise are represented, respectively, by Is(r,f) and In(f). Here r is the distance from the source to the receiving system, and f is the frequency of the signal. In relation to the previously accepted terminology [Miasnikov, 1993],
Is(r,f)=Is(r=1 m,f) T(r,f) (A2.1)
where SL(f)=10 log [Is(r=1 m,f)] - source level
TL(f)=10 log [T(r,f)] - propagation loss
NL(f)= 10 log [In (f)] - level of ambient noise
After passing through spatial and frequency filters, the signal level S and the noise N become equal to:
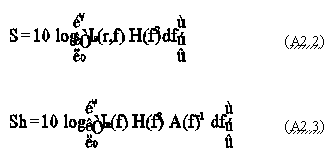
where H(f) - frequency characteristic of the filter
AG=10 log [A(f)] - array gain.
With given values for the probability of correct detection Pd and false alarm rate Pf as well as the signal integration time t, one may define the detection threshold as being
DT = 5 log[D t-1 w-1] (A2.4)
Here D is the index of detection, which is a function of the probability of correct detection and the false alarm rate, and w is the effective frequency band which is defined as
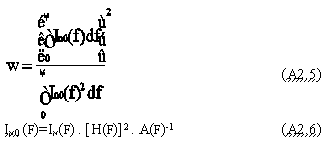
Therefore, the problem of calculating detection ranges is reduced to determining the regions of the values for r where the signal level exceeds the noise level at a given value for the detection threshold.
S-N>DT (A2.7)
In this region of values for r, correct detection will occur at a probability not less than Pd and false detection with a probability not greater than Pf.
Model of a submarine's noise level
For wide band processing of sound signals in shallow waters, the frequency band from 200 Hz to 10 kHz is of practical interest. Based on the estimates made in Appendix 1, in this frequency band the noise level of a submarine may be approximated by the equation:
SL (r=1 m, f) = SL (r=1 m, f=1000 Hz)-20 log[f/1000] (P2.8)
Values for SL (r=1 m, f=1000 Hz) for different SSBN designs are shown in Table A2. Therefore, estimates on the detection distance will correspond to the lowest noise mode for submarines ("ultraquiet operation").
We mention that contrary to our previous work, we will not consider "additional" losses, instead suggesting that they equal 0. The "additional" losses factor is related to losses through technical implementation of signal processing algorithms, imprecise a priori knowledge on the environment for sound propagation, and operator errors. As we previously noted, "additional losses" can amount to 5 to 10 dB. If this factor is considered then the estimated results for detection ranges will actually correspond to a noisier mode, i.e., a patrol at speed of nearly 8 knots (see Appendix 1).
Model for Sound Propagation Losses
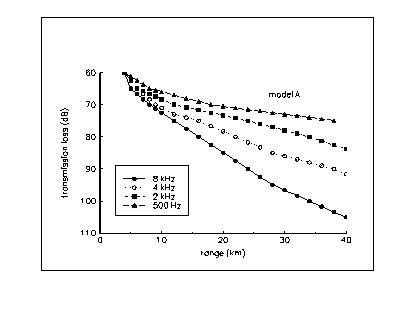
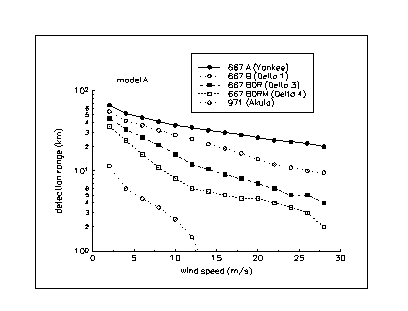
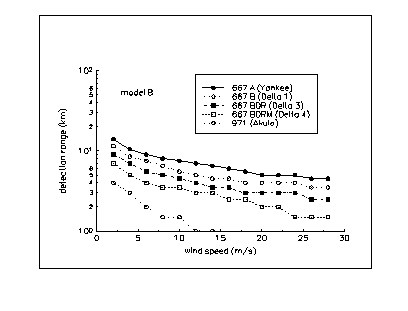
The magnitude for propagation losses varies in shallow water within a sufficiently wide range even at a fixed frequency. The vertical profile of the speed of sound, the ocean bottom, the conditions on the ocean's surface, mutual location of the source and receptors by depth all influence the conditions for sound propagation. We used two models for our estimates (models A and B) which were close to extreme situations - the most and least favorable conditions for sound propagation. The losses were dependent on propagation at several frequencies (represented in Figure A2.1 a and b) for each of these models.(30)
Nevertheless, it is correct to suggest that with wind speeds greater than 10-15 m/s, propagation losses at frequencies greater than 2 kHz will be even higher than the results in Figure A2.1. This is due to stronger damping of sound reflected from a choppy (agitated) surface. Therefore our estimates of the detection distance with great wind speeds will be somewhat too high.
Model of external noise
We assumed that the spectral density of noise is not dependent on frequencies in the 200-500 Hz band and falls off 13 dB per order of magnitude at a frequency greater than 500 Hz. Several authors note that a greater dependence on frequency proportional to 16-20 dB per order of magnitude [Wille, 1985]. Therefore, our model may actually underestimate the noise level at frequencies greater than 1 kHz and that results in estimated detection distances are overestimated.
Our model also assumes that the noise level was proportional to the wind velocity squared and the form of the noise spectrum did not depend on it [Wille, 1985].
For 200 Hz < f < 500 Hz,
NL (f) = NL (f=200 Hz, V=2.5 m/s) + 20 log [V/2.5] (A2.9)
For f > 500 Hz
NL(f) = NL (f=200 Hz, V=2.5 m/s) + 20 log [V/2.5] -13 log [f/500]
Where NL(f=200 Hz, V=2.5 m/s) = 60 dB relative to 1Pa in 1 Hz frequency band.
Model of array gain
The characteristics of the sonar antenna of a "Los Angeles" class nuclear submarine were presented in our previous work [Miasnikov, 1993]. The same sonar model was used in the present calculations of the array gain. We suggested that the array gain increased proportionally to the square of the frequency in the 200 Hz-6.6 kHz band, i.e., proportionally to the maximum number of receivers of the spherical antenna for which external noise is not correlated. On frequencies greater than 6.6 kHz it is assumed to be equal 30 dB, i.e., the value that can be maximally attained in shallow water.
We note that these estimates of the sonar amplification coefficient are somewhat higher in comparison to those which may be realized in practice. This factor will also "work" on overestimating the estimates of detection ranges.
Model of the frequency filter
The frequency characteristic of the filter, by which we achieved the maximum value in the signal/noise ratio, may be expressed in the following equation [Burdic, 1991]
[H(f)]2 = Is(r,f). A(f)2 . In(f)-2 (A2.10)
When estimating the detection ranges we modeled the optimal filter in accordance with the cited equation. Since the frequency characteristic for the optimal filter is dependent on the distance from the receiver to the source, for an estimate we used an interactive procedure, and calculated the maximum value for r which satisfies for the inequality (A2.7).
Parameters for defining the detection threshold
In our present work, we consider the detection index d=20, which corresponds to the probability of correct detection Pd=0.8 and false alarms Pf=10-4.
The integration time was maximized and was equal to nearly 100 s. This estimate corresponds to conditions when the distance from the source to the receiver does not exceed 10-20 km. With longer integration times at such distances it is not possible to disregard: a) changes in the relative location of the source and receiver in the process of registering the signal, b) changes in the conditions of sound propagation in the environment, and c) non-stationarity of ambient noise.
In practice, it is not possible to simultaneously achieve the maximum attainable array gain and signal integration time. Therefore, the choice of integration time that was made also results in an overestimated detection range compared to that which can be achieved in practice.
Commentary on estimated submarine detection ranges
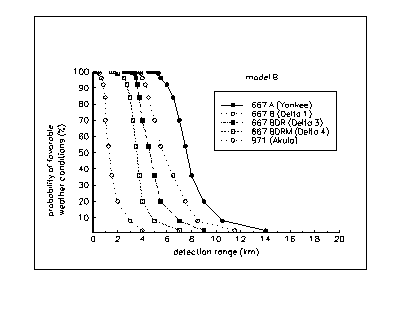
Figure A2.2 (a)-(b) show the results of the calculations of strategic submarines' detection ranges depending on the wind velocity in two situations: the most and least favorable conditions for sound propagation in shallow water (models A and B). Calculations were made in accordance with the methodologies and models discussed above.
It is interesting to compare these results with the estimates of the maximum submarine detection range using narrow band filtration (see Table A3). Overall, both methods give estimates of the same order of magnitude. Evidently, in shallow water wide-band signal processing is preferable for detecting third generation SSBNs as it indicates a larger detection range.
We again stress that estimates which were made in Appendix 2 overestimated the detection ranges. The difference between our estimates and the actual achieved detection ranges are greatest when wind speeds are more than 10-15 m/s.
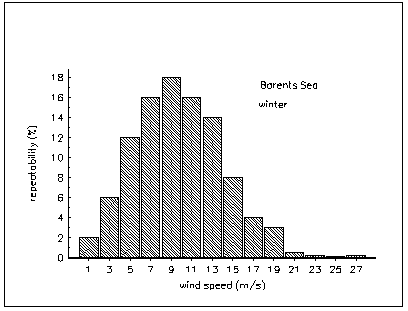
Figure A2.3 gives statistical data on observations made over many years on the repeatability of wind speeds during winter in the Barents sea area (this was limited to the 73 and 77 N and 25 and 55 E) [Wind and waves, 1974]. The repeatability of external noise levels and of the corresponding maximally achieved detection ranges were calculated using this data.
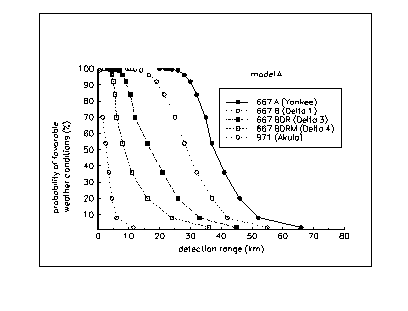
The meaning of the graphs, which are shown in Figure A2.4 (a) and (b), is sufficiently straightforward. The x-axis is the maximum detection range which corresponds to a given wind speeds V. The number on the y-axis is the probability that the wind speed does not exceed V. For example, based on Figure A2.4 (a), we can conclude that the detection range for the strategic submarine design 667 B (Delta I) in shallow waters under favorable conditions for sound propagation will not exceed 40 km - in 15% of the naturally occurring situations, 30 km - in 40% of the naturally occurring situations, and 20 km - in 92% of the naturally occurring situations.
Table A3. Estimates of the maximum detection range of Russian SSBNs in their patrol regions during the most favorable weather conditions.
| design number | ocean (km)(31) | shallow water (km) | Arctic (km) |
|---|---|---|---|
| AV 611 | >1000 | 100 | 200 |
| 629 | 1000 | 50 | 100 |
| 658 | >1000 | 100 | 200 |
| 667 A | >1000 | 100 | 200 |
| 667 B | <260-320 | 60 | 80 |
| 667 BD | <260-320 | 60 | 80 |
| 667 BDR | <130-200 | 30 | 50 |
| 941 | <130-200 | 20 | 40 |
| 667 BDRM | <65 | <15 | 5-40 |
| SSBN yr. 2000 | <5 | < 5 | <5 |
Continuous tracking of submarines: at what distances is this possible?
We were interested in the following question: at what minimum detection range can an enemy attack submarine carry out continuos secret tracking without risking a collision with a Russian strategic submarine?
To carry out secret tracking, an enemy nuclear submarine must constantly be in some "corridor" of distances to the target. The upper limit, obviously, is actually the detection range and is located below our estimates. The lower limit of this "corridor" is determined by two factors: a) tracking a target stops being secret (strategic submarine may take notice of the "tail" and take evasive measures), and b) the error in localizing the target may be comparable with the distance to the target which sharply increases the risk of collisions. It is not difficult to estimate that with detection ranges at several tens of kilometers, the width of the "corridor" may be no less than 5-10 km; and with detection distances of less than 5 km, it decreases to 1-2 km.
In this connection we stress the importance of the circumstances which will not depend on the enemy.
Firstly, during the tracking process, both the conditions for sound propagation and the level of external noise will change. Shallow water regions are characterized by fluctuations in propagation losses which reach up to 5 dB. In particular, an average detection range of 5 km will result in the upper limit "corridor" fluctuating from 2-3 to 8-9 km (model A). The tracking submarine will hardly be able to respond adequately to such changes during long periods of weeks and months.
Secondly, the strategic submarine may also change the mode of its movement. We propose that it will change to another depth. As a result the algorithm for the signal filtration will stop being optimal and the tracking submarine may lose its target. Frequently submarine collisions result from one of them changing their operating mode.
At small distances, in which tracking takes place, the integration time (the time needed for accumulating information on the signal in order to decide that a target is detected) is very important. Our calculations assumed an integration time of 100 seconds. Even if the tracked submarine moves at a minimum speed of 5 knots (2.5 m/s), during the time it takes to accumulate the signal, it has moved 250 m before changes in the target's behavior are detected. Obviously, with such a method for signal processing, attempting to tail at short distances is simply dangerous. Decreasing the accumulation time to 10 s results in the "dead distance" being decreased to 25 m, but by doing this the detection threshold is raised by 5 dB (see formula A2.4) and this leads to a reduction in the maximum achieved detection range. If in our computation the detection distance is 10 km, then with a 10 second accumulation, it is lowered to 6 km (model A). If it reached 5 km, then an increase in the detection threshold by 5 dB is equivalent to a decrease in the maximum distance to 2-3 km.
One of the biggest problems that occurs during tracking is localizing the target with the necessary accuracy. At short distances (less than 5 km), the precision for determining the distance to the target must be no worse than 0.2-0.5 km. To provide such accuracy the enemy will have to have good knowledge of the conditions for signal propagation in a specific region of military activity within a given period.(32)
Horizontal inhomogenities in the environment will lead to fluctuations in the conditions for signal propagation so that the lower limit of the "corridor" will also fluctuate because of changes in the accuracy of localizing the target.
The reasons cited permit the claim that an estimate of the detection distance at 10 km is the limit at which it is technically possible to realize continuous tracking, while ensuring covertness and guaranteeing the potential of avoiding collisions. If this is true then it is possible to see (see Figure A2.2a, A2.4a), that even in the most favorable conditions for sound propagation the "Los Angeles" class submarine can not execute this task.
Bibliography for Appendix 2
[Wind and waves..., 1974] Wind and waves in the ocean and seas, Information office. USSR registry, "Transport" Leningrad, 1974, p.94
[Miasnikov, 1993] E.V. Miasnikov, "Can Russian strategic submarines survive at sea? The fundamental limits of passive acoustics", Science and Global Security, 1994, vol. 4, p.213-251
[Akal, 1980] Tancay Akal, "Sea Floor Effects on Shallow-Water Acoustic Propagation," Bottom Interacting Ocean Acoustics, Ed. by Kuperman and F.B. Jensen, Plenum press, New York, 1980, pp. 557-575
[Burdic, 1991] William S. Burdic, Underwater Acoustic System Analysis, Prentice Hall, Inc., New Jersey, 1991, pp. 428-433
[Wille, 1985] Peter C. Wille, "Ambient Noise: Characteristics of the Noise Field" Adaptive Methods in Underwater Acoustics, Ed. by H.G. Urban, D. Reidel Publishing company, 1985, pp.13-36
28. We define the sea as shallow, if its depth does not exceed 400 m. All Arctic seas off the northern borders of Russia are shallow by this definition.
29. See Burdic (1991) for details.
30. Data were taken from Akal (1980).
31. Large detection distances occur in open ocean due to so called convergence zones (zones, at which sound rays of a given source are focused and its audibility sharply increases). A term "far zones of acoustic illumination (DZAO)" is frequently used in the Russian literature as well. Typically, the convergence zones are located at intervals of 55 to 65 kilometers. The width of the first zone is roughly several kilometers, the second zone is two times wider than the first, and so on until eventually, at ranges of several hundred kilometers, the zones overlap and become indistinguishable.
32.
Incidently, one of the goals of systematic visits by foreign SSNs to the seas around Russian territory is
gathering hydrophysical data on specific areas and the seasonal, temporal, and spatial variability of this data.