 Damage Control Training
Damage Control TrainingStability and Buoyancy Lessons
 Damage Control Training
Damage Control TrainingLESSON TOPIC: 4.1 TITLE: PRINCIPLES OF STABILITY
Contact periods allotted this LESSON TOPIC:
Classroom: 2.5 Test: 0.0
Trainer: 0.5 Total: 3.0
MEDIA: Classroom lecture with visual media, FFG-7 Stability Trainer
TERMINAL OBJECTIVES:
6.0 EVALUATE shipboard stability by analyzing weight and moment considerations. (JTI 3.2.1, 6.0, 6.1, 6.2)
ENABLING OBJECTIVES:
6.1 DESCRIBE the reference points, forces, and linear measurements used in stability calculations.
6.2 DESCRIBE the movement of stability reference points as a function of changes in displacement and inclination.
6.3 DIFFERENTIATE between indicators of initial stability and measures of overall stability as a function of ships displacement.
6.4 IDENTIFY and DESCRIBE the uses of various types of external hull markings.
6.5 Given a draft diagram/functions of form and a set of draft readings, CALCULATE displacement (WF), tons per inch immersion (TPI), and moment to trim one inch (MT1").
6.6 Given cross curves of stability and the ship's displacement, CONSTRUCT an uncorrected, statical stability curve.
FUNDAMENTALS OF STABILITY
Stability is the tendency of a vessel to rotate one way or the other when forcibly inclined. Stability can be broken down into several categories, each of which are alternatively emphasized in designing and operating Navy and Coast Guard ships.
STABILITY
INITIAL STABILITY - The stability of a ship in the range from 0° to 7°/10° of inclination.
OVERALL STABILITY - A general measure of a ship's ability to resist capsizing in a given condition of loading.
DYNAMIC STABILITY - The work done in heeling a ship to a given angle of heel.
THE LAWS OF BUOYANCY
1. Floating objects possess the property of buoyancy.
2. A floating body displaces a volume of water equal in weight to the weight of the body.
3. A body immersed (or floating) in water will be buoyed up by a force equal to the weight of the water displaced.
EXAMPLE OF GRAVITY -VS- BUOYANCY
|
|
|
1 ton of steel 1 ton of steel
If the cube of steel is placed in water it sinks. There is not enough displaced volume for the forces of buoyancy to act upon. If the ship’s hull is placed in the water it will float. The larger volume of the ship's hull allows the forces of buoyancy to support the hull's weight.
The ship's hull will sink to a draft where the forces of buoyancy and the forces of gravity are equal.
DISPLACEMENT
The weight of the volume of water that is displaced by the underwater portion of the hull is equal to the weight of the ship. This is known as a ship's displacement. The unit of measurement for displacement is the Long Ton (1 LT = 2240 LBS).
GRAVITY
The force of gravity acts vertically downward through the ship's center of gravity. The magnitude of the force depends on the ship's total weight.
UNITS OF MEASURE
Force: A push or pull that tends to produce motion or a change in motion. Units: tons, pounds, Newtons, etc.
Parallel forces may be mathematically summed to produce one "Net Force" considered to act through one point.
Weight: The force of gravity acting on a body. This force acts towards the center of the earth. Units: tons, pounds, kilograms, etc.
Moment: The tendency of a force to produce a rotation about a pivot point. This works like a torque wrench acting on a bolt. Units: foot tons, Newton meters, etc.
|
|
||
Volume: The number of cubic units in an object. Units: Cubic feet (FT3), cubic inches, etc. The volume of any compartment onboard a ship can be found using the equation:
|
|
||
Specific The specific volume of a fluid is it’s volume per unit
Volume: weight. Units: cubic feet per ton (FT3/LT). The specific volume of liquids (NSTM 096 Table 096-1) used most frequently in this unit are:
Salt Water = 35 FT3/LT
Fresh Water = 36 FT3/LT
Diesel Fuel = 43 FT3/LT
CALCULATING THE WEIGHT OF FLOODING WATER
A compartment has the following dimensions:
Length = 20 FT Flooded with salt
Breadth = 20 FT water to a depth
Height = 8 FT of 6 FT
1. First, calculate the volume of water that has been added to the compartment.
Volume = Length x Breadth x Depth of Flooding Water
= 20 FT x 20 FT x 6 FT
= 2400 FT3
2. Second, divide the volume of water by it’s specific volume.
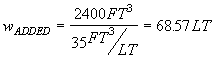
STABILITY REFERENCE POINTS
|
|
M - Metacenter
G - Center of Gravity
B - Center of Buoyancy
K - Keel |
K - Keel: The base line reference point from which all other reference point measurements are compared.
B - Center of Buoyancy: The geometric center of the ship's underwater hull body. It is the point at which all the forces of buoyancy may be considered to act in a vertically upward direction. |
|
The Center of Buoyancy will move as the shape of the underwater portion of the hull body changes. When the ship rolls to starboard, "B" moves to starboard, and when the ship rolls to port, "B" moves to port.
|
|
When the ship's hull is made heavier, the drafts increase as the ship sits deeper in the water. "B" will move up.
When the ship's hull is lightened, the drafts decrease as the ship sits shallower in the water. "B" will move down.
|
** The Center of Buoyancy moves in the same direction as the ship’s waterline. ** |
|
G - Center of Gravity: The point at which all forces of gravity acting on the ship can be considered to act. "G" is the center of mass of the vessel. The position of "G" is dependent upon the distribution of weights within the ship. As the distribution of weights is altered, the position of "G" will react as follows: |
|
|
1. "G" moves towards a weight addition 2. "G" moves away from a weight removal 3. "G" moves in the same direction as a weight shift |
||
M - Metacenter: As the ship is inclined through small angles of heel, the lines of buoyant force intersect at a point called the metacenter. As the ship is inclined, the center of buoyancy moves in an arc as it continues to seek the geometric center of the underwater hull body. This arc describes the metacentric radius. |
|
|
As the ship continues to heel in excess of 7-10 degrees, the metacenter will move as shown. |
|
The position of the metacenter is a function of the position of the center of buoyancy, thus a function of the displacement of the ship. The position of "M" moves as follows:
|
As the Center of Buoyancy moves up, the Metacenter moves down. As the Center of Buoyancy moves down, the Metacenter moves up. |
||
LINEAR MEASUREMENTS IN STABILITY
|
|
KG - Height of the ship’s Center of Gravity the above Keel: This measurement is found in section II(a) of the DC Book for several conditions of loading. To find "KG" for loading conditions other than those in the DC Book, calculations must be performed.
KM - Height of Metacenter above the Keel: This measurement is found by using the Draft Diagram and Functions of Form Curves located in section II(a) of the DC Book.
GM - Metacentric Height: This measurement is calculated by subtracting KG from KM (GM = KM - KG). GM is a measure of the ship's initial stability.
BM - Metacentric Radius: The distance between the Center of Buoyancy and the Metacenter. It is actually the radius of the circle for the movements of "B" at small angles of heel.
THE STABILITY TRIANGLE
When a ship is inclined, the center of buoyancy shifts off centerline while the center of gravity remains in the same location. Since the forces of buoyancy and gravity are equal and act along parallel lines, but in opposite directions, a rotation is developed. This is called a couple, two moments acting simultaneously to produce rotation. This rotation returns the ship to where the forces of buoyancy and gravity balance out.
|
|
|
The distance between the forces of buoyancy and gravity is known as the ship’s righting arm. As shown above, the righting arm is a perpendicular line drawn from the center of gravity to the point of intersection on the force of buoyancy line.
For small angles of heel (0o through 7o to 10o, metacenter doesn’t move), the value for the ship’s righting arm (GZ) may be found by using trigonometry:
|
|
|
Using the Sine function to solve for the righting arm:
|
|
||
With initial stability (0o to 7o-10o) the metacenter does not move, and the Sine function is almost linear (a straight line.) Therefore, the size of the ship’s Righting Arm, GZ, is directly proportional to the size of the ship’s Metacentric Height, GM. Thus, GM is a good measure of the ship’s initial stability.
RIGHTING MOMENT (RM)
The Righting Moment is the best measure of a ship's overall stability. It describes the ship's true tendency to resist inclination and return to equilibrium. The Righting Moment is equal to the ship’s Righting Arm multiplied by the ship’s displacement.
|
|
||
Example:
A destroyer displaces 6000 LT and has a righting arm of 2.4 FT when inclined to 40 degrees. What is the ship’s Righting Moment?
RM = 2.4 FT x 6000 LT
RM = 14,400 FT-Tons (pronounced "foot tons")
STABILITY CONDITIONS
The positions of Gravity and the Metacenter will indicate the initial stability of a ship. Following damage, the ship will assume one of the following three stability conditions:
|
POSITIVE STABILITY The metacenter is located above the ship’s center of gravity. As the ship is inclined, Righting Arms are created which tend to return the ship to it’s original, vertical position.
|
|
|
NEUTRAL STABILITY The metacenter and the ship’s center of gravity are in the same location. As the ship is inclined, no Righting Arms are created. (until the metacenter starts to move after the ship is inclined past 7o-10o)
|
|
|
NEGATIVE STABILITY The ship’s center of gravity is located above the metacenter. As the ship is inclined, negative Righting Arms (called upsetting arms) are created which tend to capsize the ship. |
|
STATICAL STABILITY CURVE (RIGHTING ARM CURVE)
When a ship is inclined through all angles of heel, and the righting arm for each angle is measured, the statical stability curve is produced. This curve is a "snapshot" of the ship's stability at that particular loading condition.
|
|
Much information can be obtained from this curve, including:
Range of Stability: This ship will generate Righting Arms when inclined from 0o to approximately 74o. (This curve usually assumes that the entire superstructure is watertight.)
Maximum Righting Arm: The largest separation between the forces of buoyancy and gravity. This is where the ship exerts the most energy to right itself.
Angle of Maximum Righting Arm: The angle of inclination where the maximum Righting Arm occurs.
Danger Angle: One half the angle of the maximum Righting Arm.
SHIP'S HULL MARKINGS
Calculative Draft Marks
Used for determining displacement and other properties of the ship for stability and damage control. These draft marks indicate the depth of the keel (baseline) below the waterline.
Two possible marking systems:
a. Roman numerals 3" in height (prior to 1972)
b. Arabic numerals 6" in height
Navigational Draft Marks
Ship’s operating drafts. These draft marks include the depth of any projections below the keel of the ship.
a. Arabic numerals 6" in height
Limiting Draft Marks
"...installed on those ships whose limiting displacements are known. As limiting displacements are determined, such markings will be installed. If such drafts are exceeded, it means jeopardizing the ship's ability to survive damage or heavy weather." (NSTM 079 - 14.26)
Limiting drafts are assigned to maintain reserve buoyancy (freeboard) prior to damage, and to prevent excessive hull stresses as a result of overloading.
Plimsoll Marks (Load lines)
Markings of minimum allowable freeboard for registered cargo-carrying ships. Located amidships on both the port and starboard sides the ship.
Since the required minimum freeboard varies with water density and severity of weather, different markings are used for:
- TF - Tropical Fresh Water
- F - Fresh Water
- T - Tropical Water (sea water)
- S - Standard Summer
- W - Winter
- WNA - Winter North Atlantic
|
|
DRAFT DIAGRAM AND FUNCTIONS OF FORM
The Draft Diagram is a nomogram located in section II(a) of the Damage Control Book. Each ship platform will have its own Draft Diagram and it may vary between individual ships. It is used for determining the ship’s displacement, as well as other properties of the ship, including:
- Moment to Trim One Inch (MT1")
- Tons per Inch Immersion (TPI)
- Height of Metacenter (KM)
- Longitudinal Center of Flotation (LCF)
- Longitudinal Center of Buoyancy (LCB)
Instructions for use:
1. Draw a straight line (LINE #1) between the ship's forward and aft draft readings (use calculative drafts)
2. Where LINE #1 intersects the Displacement Curve is the ship's displacement at those given drafts.
3. Draw a horizontal line (LINE #2) through the ship's displacement. (Hint: When the forward and aft drafts are equal, the line is horizontal)
4. MT1", TPI, KM, and LCB are determined using LINE #2.
5. Draw a vertical line (LINE #3) through the ship's displacement (There is no way to ensure this line is vertical - just eyeball it.)
6. Where LINE #3 intersects the LCF Curve is the ship's LCF for the given drafts.
Example:
FFG-21 has the following drafts: Forward: 14'0" Aft: 15'6"
Find: 1. Ship's Displacement: 3600 LT
2. KM: 22.37 FT
3. MT1": 758 FT-Ton per Inch
4. TPI: 32.2 LT per Inch
5. LCB: 2.1 FT Aft of Midships
6. LCF: 24 FT Aft of Midships
|
|
CROSS CURVES OF STABILITY
The Cross Curves Of Stability are used to determine the length of the righting arm at any angle of inclination for a given displacement. Using the ship's displacement (from the Draft Diagram and Functions of Form) a statical stability curve for the ship can be constructed.
Instructions for use:
1. Enter the ship’s displacement along the horizontal axis.
2. Draw a vertical line at the ship's displacement. (Hint: "tick marks" are located along the top of the curve to assist in drawing this vertical line)
3. The displacement line will cross each "angle of inclination" curve at various points.
4. The righting arm for each angle of inclination is read along the vertical axis (left side).
5. Each righting arm is plotted at the corresponding angle of inclination on the "Statical Stability Curve Plotting Sheet" or on regular graph paper.
|
|