
 Introduction to
Naval Weapons Engineering
Introduction to
Naval Weapons EngineeringDamage Prediction

When a warhead detonates in the vicinity of a target,
we may expect that the target will be damaged to some extent.
However, there is no guarantee that the target will be destroyed
or incapacitated. There are too many factors involved that may
alter the outcome of the engagement. So it only makes sense to
talk of damage in terms of probabilities.
Probability of Kill (Pk)
In order to make sense out of the infinite spectrum of
outcomes, it is useful to view it in black-and-white terms. For
most military engagements, it only matters that the target is
removed from action. It is in this sense that the target is considered
"killed." The probability of kill (Pk) is
a statistical measure of the likelihood that the target will be
incapacitated. For a warhead, the Pk will depend on
the nature of the target, specifically how it is vulnerable to
its effects (i.e. the shock wave or fragments), and the proximity
of the warhead to the target.
The probability of kill can be defined conditionally.
For instance, we can speak of the Pk if a fragment
hits the target. To clarify the situation, the following notation
will be used when needed to express the conditional Pk:
Pk|hit = the Pk if the fragment
hits the target.
In this case the overall Pk will be the product of
two factors,
Pk = Phit Pk|hit,
where:
Phit is the probability of the fragment hitting the
target.
In practice, there may be many factors contributing to the overall
Pk. For example, the target must be detected and localized,
the weapon launched and delivered to the target and then detonate
reliably. Each of these factors will add conditional terms to
the overall Pk.
Circular Error Probable
The proximity of the warhead to the target is also statistical
in nature. We may speak of the average distance from the point
of impact and/or detonation to the target if many warheads were
launched at it. Alternatively, we may speak of the most probable
outcome from a single launch, which turns out to have the same
value. Therefore, the measure of the most probable distance from
the point of impact and/or detonation to the target is the circular
error probable (CEP). It is defined as follows:
CEP = the radius of a circle about the aim point inside of which
there is a 50% chance that the weapon will impact and/or detonate.
For the purpose of estimating the probability of kill, we will
use the CEP as the distance from the point of detonation of the
warhead to the target.
Levels of Damage
There are two ways to think of the process. In one case,
there will be varying levels of damage to the target. For instance,
the target may sustain minor damage which does not affect its
operation, or the target may be completely destroyed. In the
other view, there is some probability that the target will be
removed from operation, which is the Pk. The two views
are related, of course. For descriptive purposes, we make the
following associations:
Table 1. Levels of damage and probability of kill.
| Damage Level | Description | Pk |
| light | minor damage, some functions lost, but still capable of operation. | 0.1 |
| moderate | extensive damage, many functions lost. Operation still possible but at reduced effectiveness | 0.5 |
| heavy | unable to operate | 0.9 |
Damage Criteria for Blast Effect Warheads
There are two main ways that targets may be damaged by
blast effects: diffraction and drag loading.
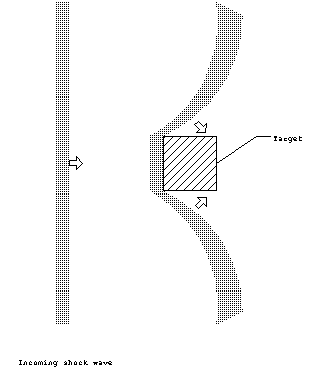
Diffraction loading is the rapid application of pressure to the
target from all sides as the shock wave passes over it. It is
associated with diffraction because the shock wave front will
bend around and engulf the target as it passes.
In diffraction loading, the overpressure of the shock wave is
applied to several sides of the object nearly simultaneously.
For instance, a square building facing the blast would feel the
shock wave arrive on the front sides and roof at nearly the same
time. Ductile targets (for example made of metal) will be crushed.
Brittle targets (for example made of concrete) will shatter.
The loading can be estimated from the peak overpressure.
Suppose a shock wave of 25 psi peak overpressure is incident upon
a standard one-story residential house. The surface area of the
house could be estimated as follows:
Front: 40 ft. x 10 ft.
Sides: 25 ft. x 10 ft.
Roof: 40 ft. x 10 ft. (front half only)
Total: 1050 ft2 x (144 in2/ft2)
= 151,200 in2
The total loading if all the peak overpressure were applied
simultaneously to the front, sides and roof would be:
Load = 25 psi x 151,200 in2 = 3.8 x 106
lb.
That's roughly 1850 tons of load. It's highly unlikely the structure
would survive.
Drag loading comes from dynamic pressure. It is the aerodynamic
force which acts on surfaces which are perpendicular to the shock
wave front. For example, if we subject the same residential structure
to 3 psi of dynamic pressure, it would feel a drag load of:
Drag load = 3 psi x 400 ft2 x 144 in2/ft2
= 172,800 lb. or
Drag load = 86 tons
In general, the drag load will be much less than the diffraction
loading. However it is applied for a longer period of time.
The drag load also reverses direction which tends to rip objects
apart.
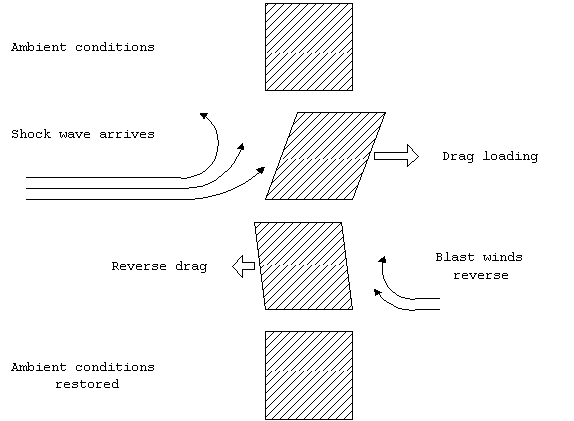
Figure 2. Drag loading.
Some targets which are relatively flexible are not damaged by
diffraction loading. These same targets may be vulnerable to
drag loading damage. Targets which are not rigidly affixed will
be thrown by the force and may be displaced by several meters.
Personnel are very vulnerable to this type of damage as well
as the secondary threat of being hit by other objects and debris
thrown by the blast. Aircraft and light equipment are also likely
to be damaged by drag loading.
For purely academic purposes, here is a table of possible
targets which indicates which effect they are most vulnerable
to and the values of peak overpressure or dynamic pressure required
to achieve three levels of damage.
Table 2. Sample damage criteria for blast effects.
| Target | Damage mechanism | Light | Moderate | Heavy |
| Industrial buildings | Diffraction | 3 | 5 |
15 |
| Roads and Bridges | Diffraction | 5 | 8 |
12 |
| Light armor | Drag | 1 | 4 |
7 |
| Heavy armor | Diffraction | 10 | 100 | 200 |
| Troops in open field | Drag | 1 | 3 |
5 |
| Troops in bunkers | Diffraction | 5 | 30 |
100 |
| Shallow buried structures | Diffraction | 30 | 175 | 300 |
| Parked aircraft | Drag | 0.7 | 1.5 | 3 |
| Ships | Drag | 2 | 5 |
7 |
Example: find the distance to which light armor might be destroyed
from 2000 lb. TNT equivalent bomb.
Referring to the dynamic pressure vs. range curve for a reference
explosion (1 kg TNT) we find that 7 psi of dynamic pressure will
be felt at about 1.5 m.
To find the scaling factor W1/3 convert the warhead
size into kg:
2000 lb. = 910 kg TNT
W1/3 = 9101/3 = 9.7
Therefore the effect (7 psi dynamic pressure will be felt to a
range of
R = 1.5 m x 9.7 = 14.5 m
Damage Criteria for Fragmentation Warheads
As a general rule, the vulnerability of some targets to
damage caused by fragments from a warhead depends on the kinetic
energy. The initial energy can be found from the Gurney analysis
and the velocity as a function of range can be found from the
drag equation. For a typical fragment, about the size of a 120
grain, 9-mm bullet, the velocity at 200 m is about 1/3 of its
initial value, and therefore the kinetic energy is down to 10%
of its original value.
Personnel
Based on typical ballistics numbers, 100 J seems to be
the minimum lethal kinetic energy. This is roughly equivalent
to a .22 long bullet (40 grains) from a rifle at 1000 fps. The
next level of damage is at about 1000 J, which corresponds to
a .357 jacketed soft-point (158 grains) bullet at 1400 fps. This
is fairly lethal (depending exactly where it hit) to unprotected
personnel. Lastly, something around 4000 J is sufficient to penetrate
body armor. This is something like a 7.62 full metal jacket or
.30-06 armor piercing bullet (166 grains) at 2750 fps. Roughly
dividing this into three broad categories:
Light (.22 cal): 100 J.
Moderate (.357 cal.): 1000 J.
Heavy(.30-06 cal): 4000 J.
Aircraft
Aircraft are generally constructed of light metals. Giving
a conservative estimate, you could treat the aircraft skin as
the equivalent of body-armor. Thus it requires about 4000 J to
penetrate the aircraft skin.
Armored Vehicles
It is probably unwise to assume an armored vehicle could
be stopped by a fragmentation warhead. Any substantial amount
of armor would require a specialized projectile. For light armor,
saboted shells, which have a .50 cal outside shoe (sabot) containing
a .30 cal shell (penetrator) that is hardened and shaped to pierce
armor. At almost 4000 fps, this can penetrate ¾" of
steel. Armor up to about 15" can be pierced by special rounds
that weigh upwards of 3.5 kg and travel at 700 m/s (making their
kinetic energy about 850 kJ). As a crude rule of thumb, we can
estimate that it takes about 10 kJ of kinetic energy per cm of
steel in order to penetrate it. Here is a summary of the damage
criteria for targets vulnerable to fragmentation warheads.
Table 3. Sample damage criteria for fragmentation effects.
| Fragment Energy in kJ | |||
| Target | Light Damage (Pk = 0.1) | Moderate Damage (Pk = 0.5) | Heavy Damage (Pk = 0.9) |
| Personnel | 0.1 | 1 | 4 |
| Aircraft | 4 | 10 | 20 |
| Armored vehicle | 10 | 500 | 1000 |
Probable Number of Fragments Hitting the Target
It can be proven that the fragments from a typical warhead
are generally lethal at long range, far in excess of the lethal
effects from blast weapons of equivalent size. Drag reduces the
energy slowly. For example, fragments from a hand-grenade can
be dangerous to a range of about 100 m. However, the likelihood
of being struck by a fragment at 100 m is small. There are only
so many fragments that are distributed in all directions. The
average number striking a target will reduce proportionally to
1/R2, where R is the range. We can express this in
the following formula:
Nhits = A(No/4pR2)
where:
Nhits is the expected number of fragments hitting the
target;
No is the initial number of fragments from the warhead;
A is the frontal area of the target presented to the warhead;
and
R is the range of the target to the warhead.
When estimating the Pk from a fragmentation
warhead, you must take into account the number of fragments that
are expected to hit the target. Multiple hits must be handled
appropriately. To wit, the correct manipulation of probabilities.
For multiple hits the overall Pk is found from
Pk = 1 - (1-PK|hit)Nhits,
if Nhits > 1, or
Pk = Nhits Pk|hit, if Nhits
< 1
Example: find the Pk from a hand-grenade against personnel
at 2 m from the detonation, assuming there are 200 fragments at
about 3000 J each (you may neglect drag at this short distance).
The closest value Pk|hit given in
the table is 0.9 at 4000 J, so it would be reasonable to expect
a probability of some where between 0.5 and 0.9 for a single 3000
J fragment. Take 0.8 as an estimate.
Assuming a person presents about 1 m2 to the warhead,
the expected number of hits will be
Nhits = 1(200)/(4p22)=
4.
Therefore,
Pk = 1 - (0.2)4 = 0.9984.
This is a crude measure to be sure, however this calculation
suffices to proof that virtually no one 2 m from a hand grenade
will survive, which is known to be true.
Compare this, on the other hand to the Pk at 5m. Here
there will only be
Nhits = 1(200)/(4p52)
= 0.6
This can be taken directly as the probability of being
hit, so that
Pk = 0.6 x 0.8 = 0.5.
So at 5 m, a person might have a 50 % chance of survival.
Generally when discussing weapons, the range within which there
will be a 50% probability of kill is called the lethal range
of the warhead.