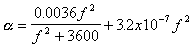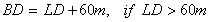Introduction to Naval Weapons Engineering

Sonar Propagation

By virtue of the fact that the speed that acoustic waves travel at depends on the properties of the medium (i.e. sea water), the propagation of sonar will be complicated. So complicated in fact that it will be impossible to accurately predict without the use of a computer model. However, sonar systems rely heavily on operator input and control to maximize their performance. Many of the decisions made regarding the maneuvering of the ship carrying the sonar system will also affect the sonar's performance. Therefore a detailed knowledge of the salient features of sonar propagation is essential to its successful employment. We begin with a simple model for the transmission loss.

Transmission Loss Formula

Transmission loss (TL) can be predicted, to a very rough degree, solely on the basis of a few factors. These factors are range, and frequency.

Range Effect

The simplest case, which is the identical case used in electro-optics and radar, is to assume all of the acoustic energy is uniformly distributed in all directions. In sonar this is termed spherical spreading loss, since the intensity will fall off proportional to the surface area of a sphere.

Figure 1. Spherical spreading.

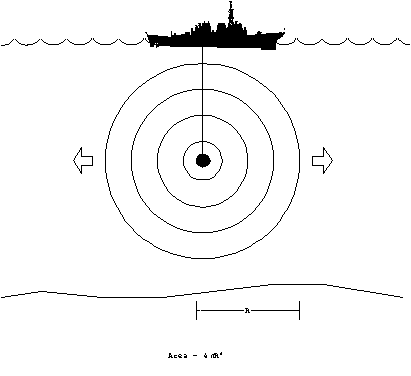
Since the area over which the energy is distributed at range, R, is 4pR², the ratio of any two intensity levels at different ranges can be computed. If we take the decibel equivalent, and take the first range as one meter, which happens to be where the source level is defined, we obtain the spherical spreading loss f part of TL:

TL_spherical = -10 Log { I(R)/I(1 m)} = -10 Log{1/R²}

TL_spherical = 20 Log(R) .

The negative sign was included since TL is defined to be positive quantity, and is subtracted in the SNR equations.

When the acoustic energy reaches either the surface or the bottom of the ocean, it is generally reflected back. A long range, all of the acoustic energy will tend to confined between two planes, one at the surface and the other at the bottom. Therefore, the energy can no longer spread out like the spherical spreading case, but now becomes cylindrical spreading.

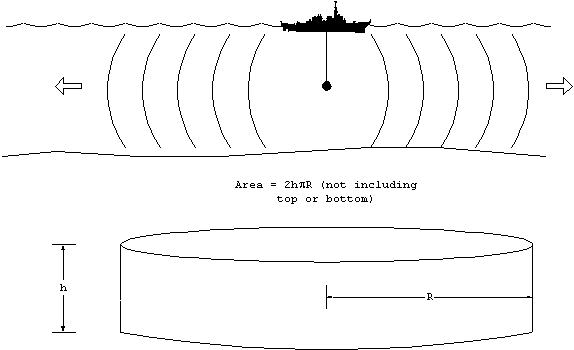
Figure 2. Cylindrical spreading.

The area over which the energy is distributed now varies directly with range, R. The common factors will cancel, and the transmission loss between two ranges will be 10 Log( R). Explicitly this means

SPL(R₂) = SPL(R₁) - 10 Log(R₂/R₁).

It would be nice if we could choose R₁ to be one meter in which case SPL(R₁) = SL, but this would be incorrect. That would be akin to claiming that the spreading losses where cylindrical starting from one meter. Clearly, in regions where the water depth is larger than the range, the spreading must be spherical.

The question now becomes: at what range does the spreading loss transition between the spherical and cylindrical case. If the source where located exactly in the middle (halfway between the surface and bottom), then it seems plausible to make the transition when the range is one-half the water depth since this is when the surface of the sphere will just touch the bottom and top. The transition range will depend on the location of the source and the depth of water. For purposes we assume the transition range to be 1000 m, since the average ocean depth is about 2000 m.

At 1000 m, the transmission loss due solely to spherical spreading will be 60 dB. Taking this as the starting point for cylindrical spreading, we can patch the two equations together by adding 30 dB to the 10 Log(R) spreading. This is proven below:

TL_spherical(at 1000 m) = 20 Log (1000) = 60 dB

TL_cylindrical(at 1000m) = 10 Log(1000) = 30 dB

If we wish to apply the TL_cylindrical formula starting at 1 m, then we must add the difference at 1000m, therefore

TL_cylindrical (R) = 10 Log(R) + 30 dB. (valid when R > 1000 m)

At ranges of less than 1000 m, you must use the spreading spreading loss formula, TL_spherical = 20 Log(R).

absorption/scattering

Like air in electro-optics, the intervening water between the source and receiver will either absorb some of the acoustic energy passing through it. The dependence on range will be identical to Bougher's law, but now in decibel form:

Tl_abs = - 10 Log( e^-bR) = (10 b)R

where b is the extinction coefficient. The factor of 10 and a unit conversion into km is absorbed in the definition of the absorption coefficient, a b/100, therefore

Tl_abs = a R.



where a has units of dB/km. The absorption coefficient has a strong frequency dependence, meaning much greater losses at higher frequency. The absorption coefficient can be calculated from a formula:




where f is in kHz, and the result for a is in dB/km.

or using a graph:

Figure 3. Absorption coefficient
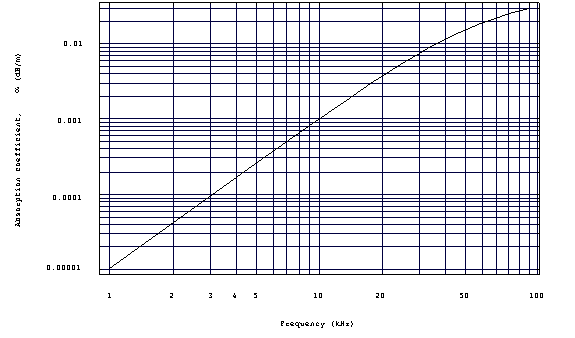
as a function of frequency.

Other losses

Many other things can happen to the acoustic wave as it propagates. For example the energy may scatter off particles or biologics. Energy will be lost upon reflection from the surface and bottom. And lastly, by but far the greatest factor of all will be the change in the propagation due to the variations in the speed with temperature, depth and salinity. The change in speed will tend to distort the perfect spherical or cylindrical shape of the wave front. This does not, however, always result in greater transmission losses. As we shall soon see, there are many conditions which tend to concentrate acoustic energy resulting in a lower than expected transmission loss.

All of these factors just discussed can be lumped into a single term, A, called the transmission loss anomaly. This is surely artificial and is only used in order to be able to write a complete equation for TL. All deviations from the predicted result can be explained away in the term A. The equation so written is

TL = 10 Log(R) + 30 + aR + A

If you ignore, the last two terms, the range dependence is very straight forward, and can be used to generate some rules of thumb:

TL 60 dB at 1 km

TL 70 dB at 10 km

TL 80 dB at 100 km.

This is based on nothing but the spherical and cylindrical spreading losses, assuming the source is exactly in the middle of 2000 m deep water. What one finds in practice, are variations about these baseline numbers. This can also be shown in graphical form, TL vs. range.

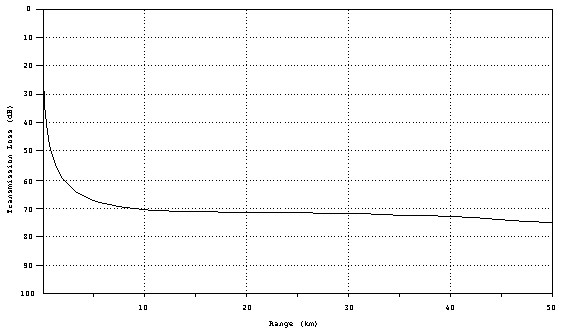
Figure 4. Geometrical
transmission loss curve.

Propagation Paths

To gain further insight into how the environment can affect propagation, we first study how the propagation speed varies in the ocean.

The Sound Velocity Profile (SVP)

The largest variation is the speed of sound in water occurs with changes is depth. Obviously the pressure increases with depth causing a uniform increase of +1.7 m/s for every 100 m. Furthermore, the ambient temperature changes with depth. A plot of propagation speed (velocity) as a function of depth, is called the sound velocity profile (SVP), and it is the fundamental tool for predicting how sound will travel. Neglecting salinity, the SVP can be obtained from sampling the ambient temperature at various depths (the pressure contribution never varies). An inexpensive probe to do this is called an expendable bathythermograph (XBT). The resulting SVP looks like this:

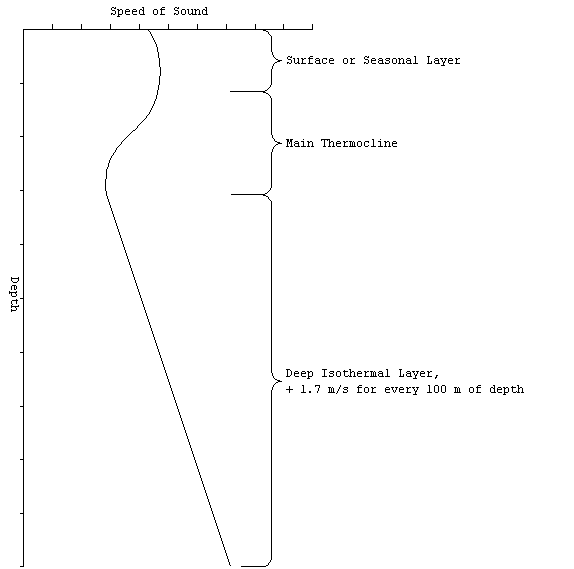
Figure 5. Oean layers.

The SVP reveals some common structure to the ocean. The water can be divided into three vertical regions.

The surface (seasonal) layer is at the top and is the most variable part. As the name suggests, the profile will changes depending on the time of day (diurnal variation) and the season (seasonal variation). During the day, the heat from the sun (insolation) causes the water at the very top to be warmer than the water below. Since the condition of warm over cold is stable, the condition is quite common. Late in the afternoon, particularly on a bright day, the surface temperture will be the greatest and so one would expect the greatest gradient (change with depth).

Figure 6. Diurnal variation in
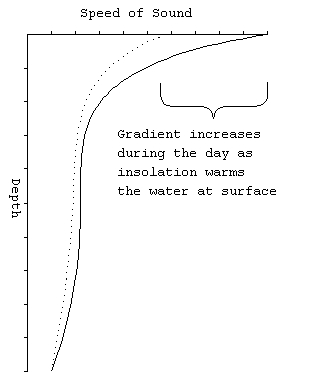
SVP.

The main thermocline connects the seasonal layer with the uniformly cold water found deep in the ocean. Below about 500 m, all of the world's oceans are at about 34^o F. The positive gradient in the deep isothermal region is solely due to the pressure effect.

In the summer, the seasonal layer tends to have a strongly negative gradient, for the same reason as given to explain the diurnal variation. So the summer profile looks like:

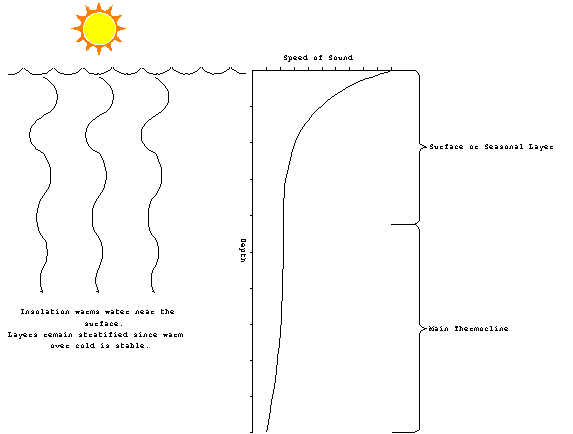
Figure 7. Summer SVP.

In winter, the water is generally warmer than the air. A lot of heat is lost through advection and radiation. However, one would not expect to see cold water setting on top of warm water for very long. Convection brings the warm water to the surface destroying the effect. The surface layer tends to be closer to isothermal than anything else. Additionally, strong winter storms and their large waves frequently mix the surface layer to a depth of up to 100 m. For the nearly isothermal surface layer, one could expect a weakly positive gradient above the main thermocline.

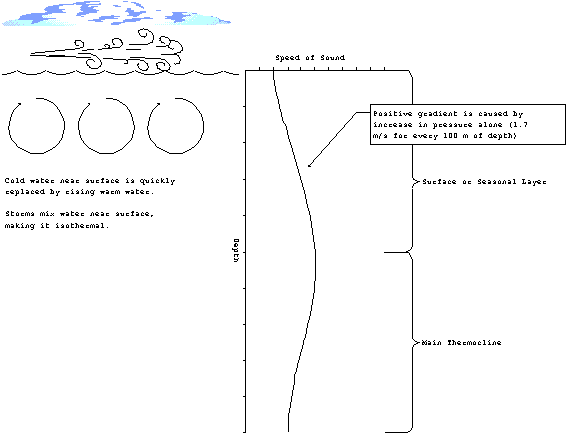
Figure 8. Winter SVP.

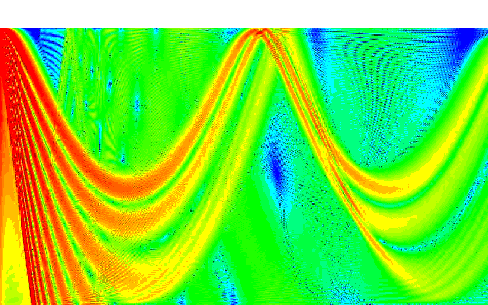
Ray Tracing

The change of propagation speed with depth will manifest itself through refraction of the sound. A graphical method of illustrating the effects is called ray tracing. The basic idea is to draw lines perpendicular to the wave fronts and follow their paths. For a typical sonar array, these lines start equally spaced within the beam capability of the array (discussed in the next chapter).

Figure 9. Ray tracing.

As the rays go deeper, they begin to refract. Recall how differences in the index of refraction (which are a measure of the propagation speed) affected electromagnetic waves. As the rays move into a medium which has a slower propagation speed, they tend to become more vertical. On the whole, the rays will deflect downward in a negative gradient.

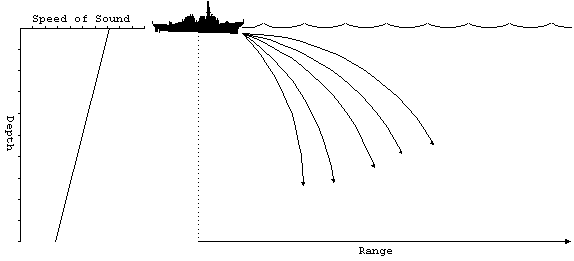
Figure 10. Negative SVP
gradient.

As you might expect, the opposite effect occurs when the gradient is positive. As the rays enter deeper water the propagation speed increases and the rays bend upwards.

Figure 11. Positive SVP gradient.


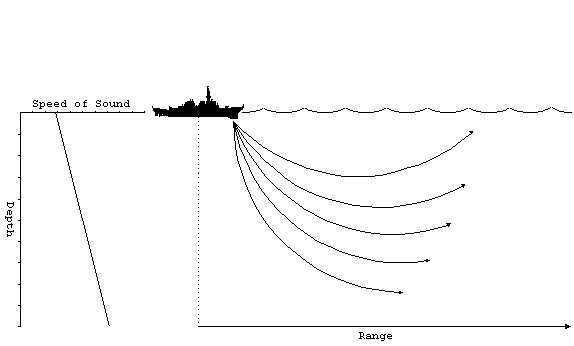
All of the rays will be deflected upwards. When the rays reach the surface, the will be reflected back downwards and the same process begins again. Naturally, some of the energy is lost and the reflection, but the overall effect is to trap the sound in a relatively small layer below the surface. The sound does not reach the deeper regions, so the transmission less than you would expect for cylindrical spreading. This effect is called a surface duct.

Figure 12. Surface duct.

The other common propagation modes occur during combinations of positive and negative gradients. A positive gradient over a negative gradient produces a special kind of propagation, where the rays split at the boundary which is called the layer. The depth of maximum sound velocity which ocurs on the layer is called the layer depth (LD).

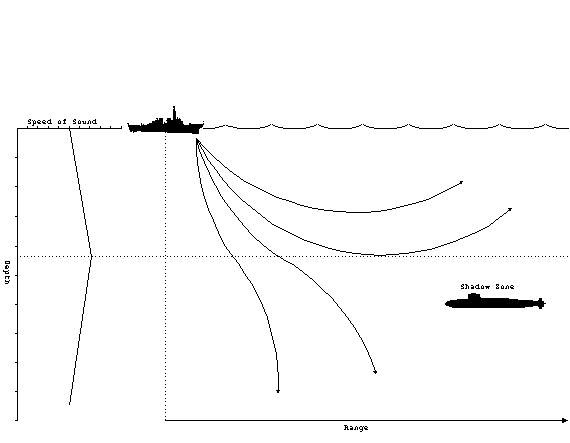
Figure 13. Sonic layer.

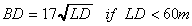
Above the layer, the positive gradient will produce a surface duct as previously described. When rays penetrate below the layer, they are deflected downward. Therefore, the rays diverge above and below the layer. Beyond a certain minimum range, the rays from the source will never reach locations just below the layer. This is called the shadow zone. It is a favored depth for submarines to operate at for just this very reason. The optimum depth to operate at, called best depth (BD), is a function of the layer depth. The best depth can be calculated from






For the case where the negative gradient is over the positive, rays which originate at the boundary will be deflected back towards the middle, regardless if they go up or down. This forms a sound channel, where the rays are then confined to the small region above and below the axis, called the sound channel axis.

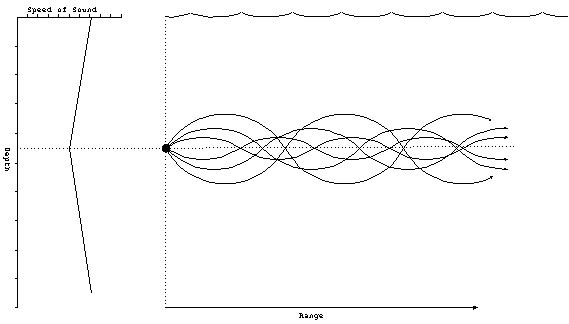
Figure 14. Sound channel.

The sound channel will not work for rays that begin at the surface, like in the other cases. The source must be located near the axis. Several sonar systems have features which allow them to be placed near the sound channel axis. For example, sonobouys, which are small self-contained sonar systems, have a setting which places them at a typical sound channel axis depth.


Another special type of propagation occurs when the water is so deep that no sound can reach the bottom without being deflected upwards by the normal positive gradient found in the deep isothermal layer. This situation requires a minimum of 200 m of depth excess which is defined as

depth excess: the distance from the lower boundary of the sound channel to the bottom.

When all of the sound rays are returned to near the surface, they tend to converge into a small region. Therefore the sound pressure level is increased dramatically in this region known as a convergence zones (CZ).

Figure 15. Convergence
zone.

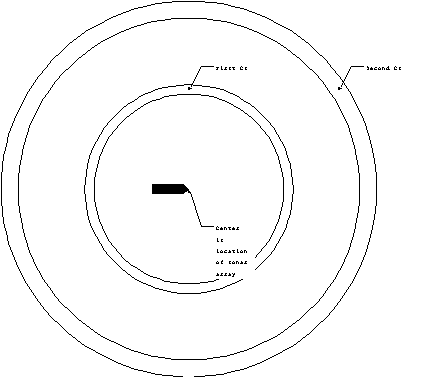
The convergence zone tends to be at large distances, typically 20-30 nm from the source. It is possible to have multiple convergence zones, which will occur at regular intervals. For example, if the first CZ is at 30 nm, the second CZ would be at 60 nm. The CZ is only a few miles wide, and therefore, contacts which are acquired through convergence zones tend to appear and disappear quickly.

It may be possible for a ship to have a rather limited sonar range due to regular transmission losses but multiple convergence zones. These zones form protective rings about the ship. A hostile submarine closing in on the ship would be detected as it passes through the various convergence zones, thereby alerting the ship to its presence. The ship could then deploy mobile ASW assets like a helicopter to handle the submarine.

Figure 16. Annulus of CZ.

Finally the last type of propagation occurs in when the sound is strongly reflected from the ocean floor. The rays tends to converge near the surface, resulting in a reduced transmission loss. This is called bottom bounce propagation. Rays from bottom bounce can be identified from the others because of the larger angle of incidence. Typical bottom bound comes into the sonar at angles of more than 30^o from horizontal.

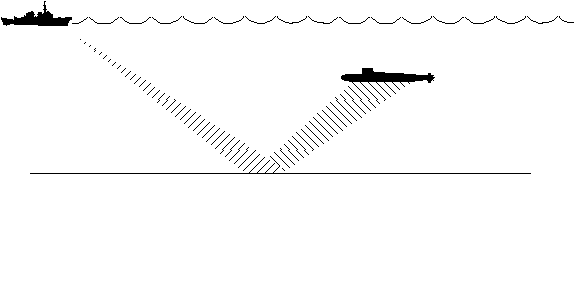
Figure 17. Bottom bounce.

Only certain ocean floor conditions are conducive to bottom bounce propagation. Flat and hard ocean floors tend to be the best. Soft mud, on the other hand is the worst.

Figure of Merit

Because the propagation of acoustics waves in the ocean is fairly complicated, the use of a formula for transmission loss is of limited accuracy. Computer models can be used to produce much more accurate plots of TL as a function of range, known as transmission loss curves. Here is a typical TL curve showing some of the features just discussed:

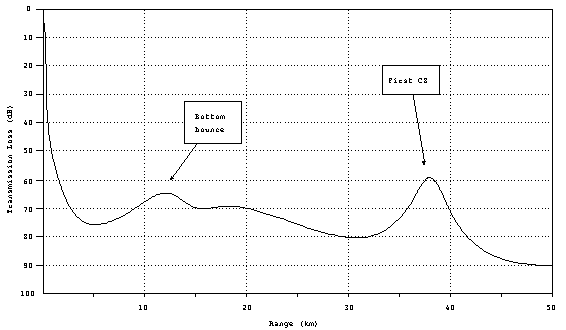
Figure 18. Typical TL
curve.

In comparision to the geometrical TL (spherical and cylindrical spreading losses) you will note there are certain ranges where the TL actually goes down with increased range. These are locations where the refraction effects of the ocean cause the sound rays to concentrate. This example illustrates the effect of bottom bound and CZ.

Given an accurate transmission loss curve, we are now in a position to estimate the maximum detection range of a sonar system. Recall that detection is possible whenever

SNR < DT.

To solve for range, we only need rearrange terms to isolate the range dependence. For the passive case, define figure of merit, FOM

FOM_passive SL + DI - NL - DT

Now the detection criterion becomes

FOM > TL.

Which leads to the following interpretation:

Figure of Merit (FOM) is the maximum transmission loss the system can have and still be able to detect the target (at 50% of the time).

If FOM is known, then the maximum range can be determined by plotting the FOM as a horizontal line on the TL curve. All ranges where the FOM > TL (remember that TL is increasing in the down direction), are detectable.

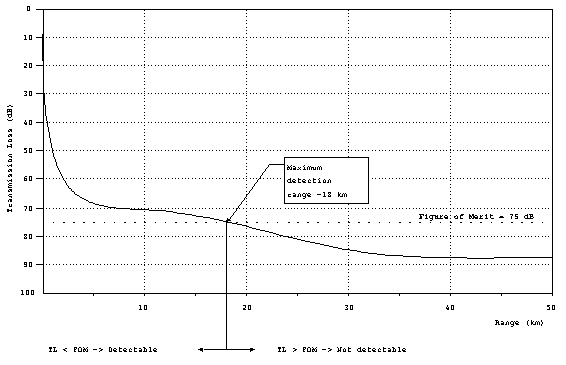
Figure 19. Determining
maximum detection range from FOM.

In this example, the FOM = 75 dB. From the graph, it is apparent that FOM > TL everywhere less than 18 km, which is the maximum detection range.

FOM_active SL + TS + DI - NL - DT

For active systems, there are (at least) two complications. First the FOM is modified so that

Secondly, the transmission loss is incurred twice, as the sound travels to the target and back. You could use a separate curve with twice the TL vs. range, or alternatively, use one-half the FOM, which is the preferred method. So for active systems, the detection criterion is:


FOM > 2 TL or FOM/2 > TL.

Therefore, you calculate FOM and then plot FOM/2 on the TL curve to obtain range in the same manner.